ÉLECTROMAGNÉTISME
Lignes de champ magnétique
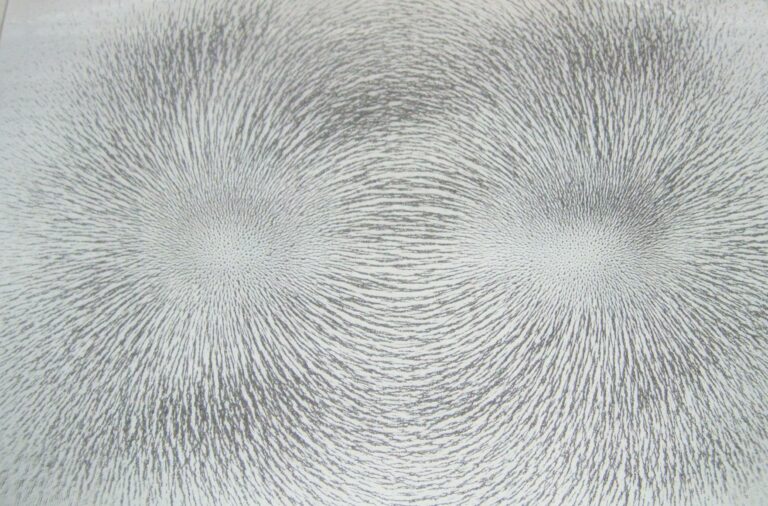
Aimant droit
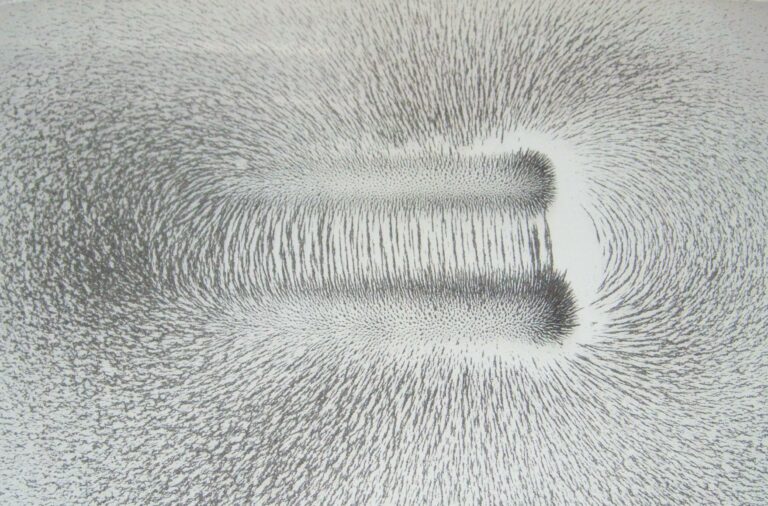
Aimant en U
Expériences Montaigne sur YouTube
Roue de Barlow et spirale de Roget
Rails de Laplace et fil de Laplace
Freinage électromagnétique : pendule plein
Freinage électromagnétique : pendule évidé
Freinage électromagnétique : pendule hachuré
Compétences et questions sur le cours
Compétences fondamentales
Équations de Maxwell
- connaître les différentes distributions de charge et l’équation locale de conservation de la charge.
- connaître par cœur les équations de Maxwell, écrire correctement les opérateurs (rotationnel et gradient s’écrivent en minuscule avec une flèche mais s’appliquent respectivement à un vecteur et à un scalaire ; divergence s’écrit en minuscule sans flèche et s’applique à un vecteur).
- connaître les différents régimes (statique, A.R.Q.S, ondulatoire) ainsi que les propriétés des équations de Maxwell (propriétés des champs selon les régimes, linéarité).
- connaître la force de Lorentz, l’énergie volumique cédée par le champ aux porteurs de charge, le théorème de Poynting, le vecteur de Poynting et la densité d’énergie électromagnétique, leur unité, leur signification, leur non linéarité vis-à-vis des champs et \overrightarrow{E} et \overrightarrow{B} .
- connaître les relations de passage.
Champ électrique stationnaire
- connaître les équations locales qui régissent les champs (M.F et M.G) et V (Poisson) en régime stationnaire, ainsi que leur version « intégrale » (à circulation conservative, théorème de Gauss).
- connaître les champs créés par une charge ponctuelle ; savoir exprimer les champs créés par des distributions volumiques, surfaciques, linéiques de charge.
- savoir utiliser les symétries / antisymétries planes pour trouver la direction de \overrightarrow{E} , les invariances des distributions pour montrer que \overrightarrow{E} ne dépend pas de certaines coordonnées.
- connaître les cas de continuité / discontinuité spatiale des champs, les relations de passage pour \overrightarrow{E} .
- connaître l’énergie électrostatique d’une charge ponctuelle dans un champ ainsi que celle d’une distribution de charges.
- connaître les propriétés topographiques de \overrightarrow{E} .
- savoir calculer \overrightarrow{E} grâce au théorème de Gauss pour des distributions de charge à symétrie cylindrique ou sphérique.
- connaître la définition d’un dipôle électrostatique, de son moment dipolaire. Connaître la technique pour trouver le champ créé par un dipôle. Connaître l’expression des actions subies par un dipôle rigide.
- savoir établir un tableau d’analogies entre les champs électrique et gravitationnel.
Condensateur
- connaître et savoir décrire le phénomène d’influence.
- connaître la définition d’un condensateur, de sa capacité. Connaître une méthode de calcul de C.
- connaître par cœur la capacité d’un condensateur plan et savoir la retrouver.
Transport de charges
- connaître le caractère conservatif de \overrightarrow{J} en régime stationnaire et la conservation de I le long d’un tube de courant.
- conducteur ohmique : connaître le modèle de Drude, la loi d’Ohm locale, la définition de la résistance, une méthode de calcul de R. Connaître par cœur la résistance d’un conducteur cylindrique.
- connaître l’expression des forces de Laplace sur un conducteur filiforme.
Champ magnétique stationnaire
- connaître les équations locales qui régissent le champ \overrightarrow{B} (M.T et M.A) en régime stationnaire, ainsi que leur version « intégrale » ( \overrightarrow{B} à flux conservatif, théorème d’Ampère).
- savoir utiliser les symétries / antisymétries planes pour trouver la direction de \overrightarrow{B} , les invariances des distributions pour montrer que \overrightarrow{B} ne dépend pas de certaines coordonnées.
- connaître les cas de continuité / discontinuité spatiale de \overrightarrow{B} , les relations de passage pour \overrightarrow{B} .
- connaître les propriétés topographiques de \overrightarrow{B} .
- savoir calculer \overrightarrow{B} grâce au théorème d’Ampère pour un solénoïde torique, un solénoïde infini droit, un fil rectiligne infini.
- connaître la définition d’un dipôle magnétique, de son moment dipolaire. Connaître, par analogie avec le dipôle électrostatique, le champ \overrightarrow{B} créé par un dipôle et l’expression des actions subies par un dipôle rigide.
- connaître la définition d’une inductance propre et mutuelle ainsi que l’expression de l’énergie magnétique d’un ensemble de circuits. Savoir démontrer M^2 \le L_1 L_2 .
Électromagnétisme dans l’A.R.Q.S
- connaître la définition de l’A.R.Q.S magnétique.
- connaître la loi de Faraday et l’expression de la f.e.m induite . Bien comprendre que \overrightarrow{E} n’est plus à circulation conservative.
- induction de Neumann : comprendre l’effet de peau dans un conducteur, l’apparition de courants de Foucault ; connaître l’expression de l’épaisseur de peau.
- induction de Lorentz : connaître l’exemple des rails de Laplace, le bilan énergétique , le fonctionnement moteur / générateur.
- savoir mettre en équation un circuit avec mutuelle inductance.
F.A.Q
Non car il ne vérifie pas \text{div}\overrightarrow{E}=0 .
Oui car il vérifie \text{div}\overrightarrow{B}=0 .
En combinant M.A et M.G . Savez-vous le faire ?
Il suffit d’utiliser l’équation de conservation de la charge et M.G. On a \tau =\frac{\epsilon_{0}}{\gamma} . Cette constante est de l’ordre de 10^{-18} \; \text{s} .
Chargé volumiquement en un point, le conducteur redevient neutre en une durée extrêmement brève. Il est décidément bien difficile d’obtenir des charges volumiques dans un conducteur.
- \overrightarrow{S_{\text{P}}}=\frac{\overrightarrow{E}\land\overrightarrow{B}}{\mu_{0}}
- C=\frac{\epsilon_{0} S}{e} où S est la surface des armatures et e la distance entre ces armatures.
- R=\frac{l}{\gamma S} où S est la section du conducteur et l sa longueur.
- \frac{\text{d}^{3}p}{\text{d}^{3}V}=\overrightarrow{J}\cdot\overrightarrow{E}
- u=u_{\text{e}}+u_{\text{m}}= \frac{\epsilon_{0}E^2}{2}+\frac{B^2}{2\mu_{0}}
pour \overrightarrow{E}:
\overrightarrow{E_{2}}-\overrightarrow{E_{1}}=\frac{\sigma}{\epsilon_{0}}\overrightarrow{N}_{1\rightarrow 2}
pour \overrightarrow{B}:
\overrightarrow{B_{2}}-\overrightarrow{B_{1}}=\mu_{0}\overrightarrow{J_{\text{S}}}\land\overrightarrow{N}_{1\rightarrow 2}
Ces expressions sont vraies à la traversée d’une distribution surfacique. Dans la cas d’une distribution volumique, le champ électromagnétique est continu.
\epsilon_{0} \simeq\frac{1}{36\pi \cdot 10^9} \;\text{F}\cdot \text{m}^{-1}
\mu_{0} \simeq 4 \pi \cdot 10^{-7} \; \text{H}\cdot \text{m}^{-1}
Un courant passe dans le disque en cuivre depuis son centre vers le bain de Hg(l). La présence d’un aimant en U permet d’obtenir un champ magnétique orthogonal au plan du disque. Ce sont donc les actions de Laplace, donc le moment est non nul, qui expliquent la rotation du disque. Si on inverse le sens du courant, le disque tourne dans l’autre sens. Ce dispositif, appelé roue de Barlow, n’est plus exhibé, tout comme le suivant, car il utilise du mercure liquide, produit toxique. C’est l’ancêtre des moteurs électriques.
Dans le cas de la spirale de Roget, c’est le champ magnétique propre de la bobine, parcourue par un courant récupéré par le mercure, qui permet l’existence de forces de Laplace. ces dernières provoquent la contraction de la spirale, quel que soit le sens du courant (comme on le verra en fin d’année). L’extrémité de la spirale ne touchant plus le mercure, le courant cesse et la spirale retombe. Le courant se rétablit alors et le processus recommence. Des étincelles apparaissent quand l’extrémité de la spirale est proche du mercure car lorsque le champ électrique dépasse une valeur de l’ordre de E_{\text{disruptif}}\simeq 4\cdot 10^6 \text{V}\cdot \; \text{m}^{-1} , l’air s’ionise.
C’est grâce au champ magnétique de l’aimant en U (approximativement vertical) que la barre se met en mouvement. selon le signe du champ magnétique et du courant, les forces de Laplace sont dirigées vers la droite ou vers la gauche.
Le fil de Laplace, placé dans le champ magnétique horizontal de l’aimant en U, subit des actions du même nom lorsqu’il est parcouru par un courant, et le sens de sa rotation dépend du sens du courant qui le parcourt.
Le pendule conducteur étant en mouvement dans un champ magnétique stationnaire, on est en présence du phénomène d’induction de Lorentz. Un champ électrique induit apparaît dans le conducteur et ainsi naissent des courants de Foucault, volumiques. Le pendule est donc soumis à des forces de Laplace dont l’expression volumique est :
\frac{\text{d}^{3}\overrightarrow{F_{\text{L}}}}{\text{d}^{3}V}=\overrightarrow{J}\land\overrightarrow{B}
D’après la loi de Lenz, le moment résultant de ces forces s’oppose au mouvement (freinage). Une partie de l’énergie mécanique est dissipée par effet Joule.
Si les courants de Foucault sont contrariés par feuilletage avec un matériau isolant ou ici en évidant ou en striant le conducteur, la puissance dissipée diminue, et le pendule est moins freiné.
Induction de Neumann : conducteur fixe dans \overrightarrow{B} variable.
Induction de Lorentz : conducteur mobile dans \overrightarrow{B} stationnaire.
Dans tous les cas, la loi de Faraday :
e=\oint_{\gamma} \overrightarrow{E} \cdot \text{d}\overrightarrow{OM} = – \frac{\text{d}\Phi}{\text{d}t}, avec:
\Phi= \iint_{S(\gamma)} \overrightarrow{B} \cdot \text{d}^2\overrightarrow{S}
est valable.