PHÉNOMÈNES DE TRANSPORT
Actions de pression dans un fluide
Actions de pression dans un fluide
Dynamique des fluides
Dynamique des fluides
Flux thermiques
Flux thermiques
Recueil de TD : Phénomènes de transport
Recueil de TD : Phénomènes de transport
Compléments de cours
Les techniques de la mécanique des fluides
Les techniques de la mécanique des fluides
Soufflerie numérique
Soufflerie numérique
Expériences Montaigne sur YouTube
Statique des fluides : mise en évidence des actions de la pression atmosphérique
Réversibilité d’un écoulement de Stokes
Écoulements 2D
Transport par diffusion thermique : métaux différents
Transport par diffusion thermique : longueurs différentes
Transport par convection thermique
Régime transitoire dans une barre
Voir exercice du TD sur la diffusion thermique : une barre de longueur L=0,1\text{ m} et de diffusivité thermique a=5\cdot 10^{-5}\text{ m}^2\cdot \text{s}^{-1} est placée entre deux solides de capacités thermiques C_1 et C_2=2C_1, de températures initiales T_1^0=100\text{ °C} et T_2^0=0°\text{C}. L’ensemble est isolé.
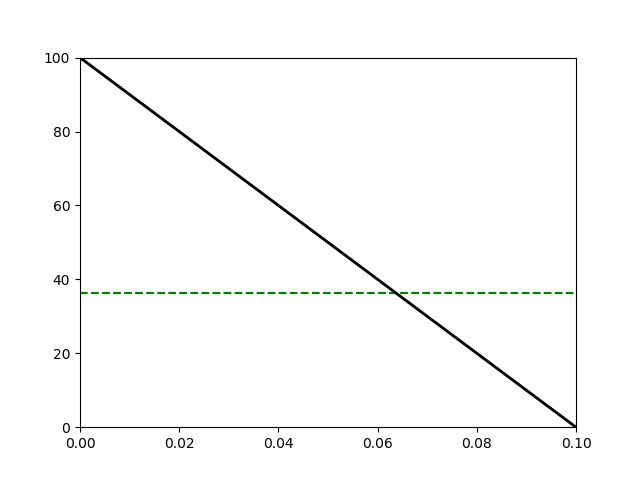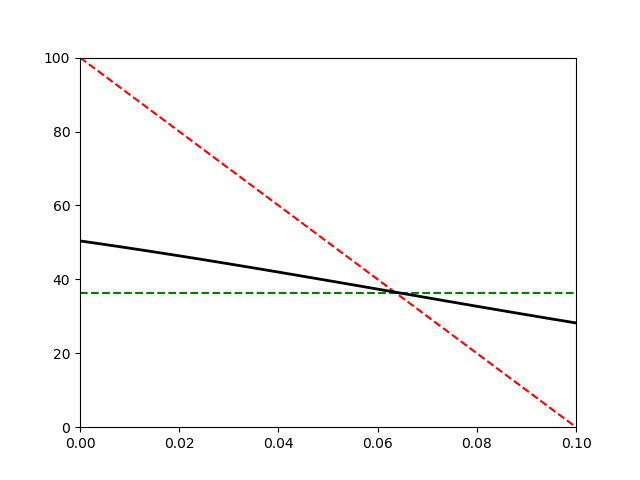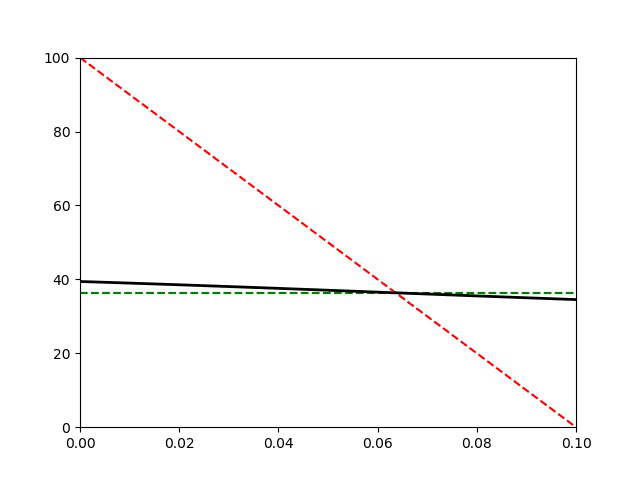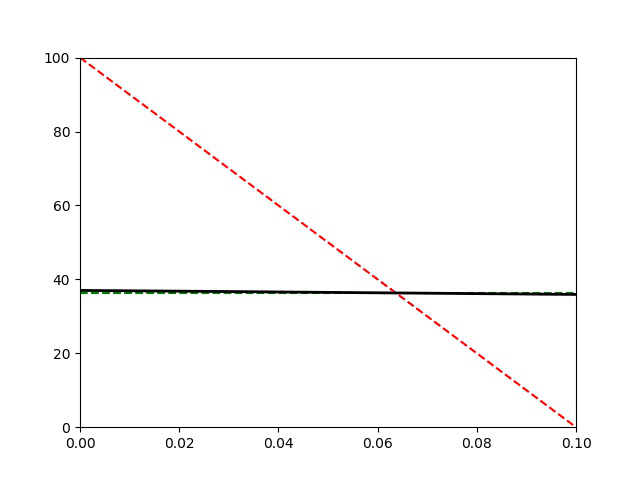
A.R.Q.S thermique : les capacités des solides sont grandes devant celle de la barre. Leurs températures varient « lentement », c’est-à-dire sur une durée \tau >> \tau_\text{d}=\frac{L^2}{a}. le profil de température dans la barre est affine à tout instant. La durée de la simulation est de 1000 s.
En réalité, pour avoir une convergence plus rapide, on a pris ici \tau = \tau_\text{d}. Le profil est encore assimilable à une droite à tout instant, mais la capacité thermique de la barre n’étant pas négligeable devant celles des solides, la température finale est supérieure à celle attendue :
T_\text{f}=\frac{T_1^0+2T_2^0}{3}=33,3\text{ °C}.
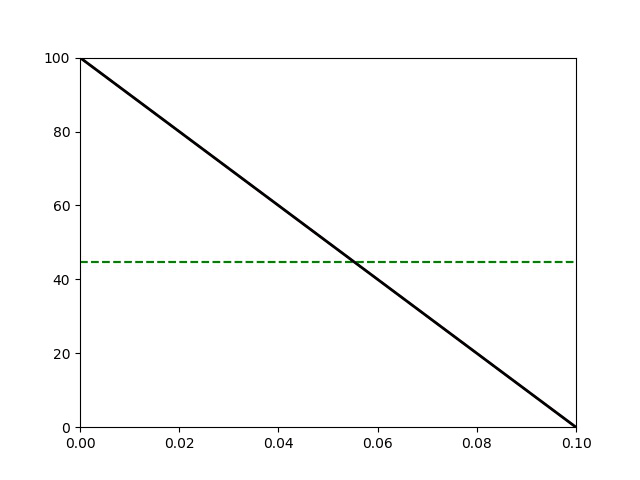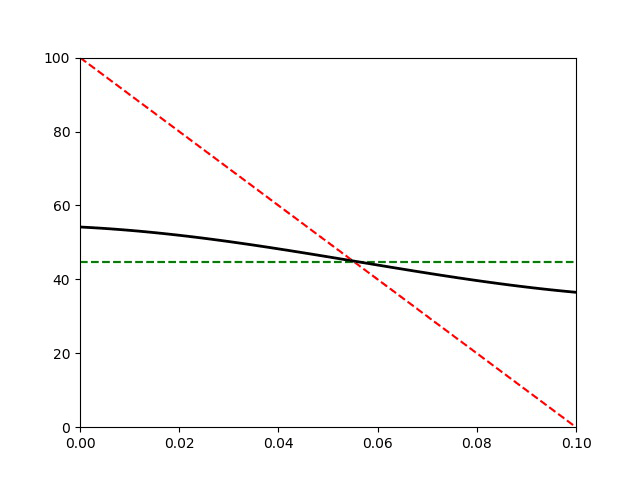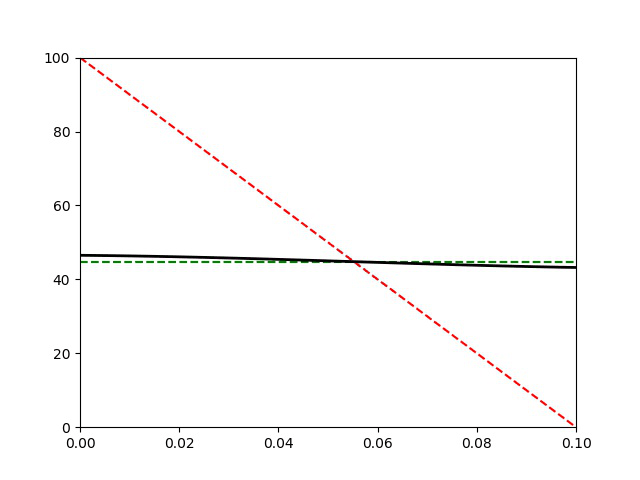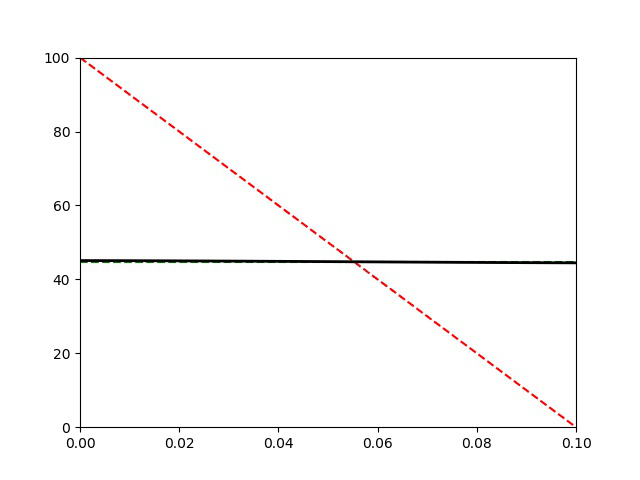
L’A.R.Q.S thermique n’est plus vérifiée car ici on a pris \tau =0,1 \tau_\text{d}. Le profil de température dans la barre n’est plus affine à un instant quelconque. La durée de la simulation est de 200 s.
La capacité thermique de la barre C étant supérieure à celle des solides, la température finale se rapproche de la valeur moyenne :
T_\text{moy}=\frac{T_1^0+T_2^0}{2}=50\text{ °C} que l’on aurait si C>>C_1,C_2.
Compétences fondamentales
Statique des fluides
● connaître les définitions de libre parcours moyen et d’échelle mésoscopique.
● identifier une force de pression comme étant une action normale à une surface ; utiliser l’équivalent volumique des forces de pression -\overrightarrow{\text{grad}}p .
● savoir exprimer la relation fondamentale de la statique dans un référentiel galiléen et en déduire le champ de pression statique dans un fluide : savoir exprimer l’évolution de la pression avec l’altitude dans les cas d’un fluide incompressible et de l’atmosphère isotherme dans le modèle du gaz parfait.
● connaître l’expression de la poussée d’Archimède ainsi que les conditions de validité de cette expression.
Description d’un fluide en mouvement
● dominer les différentes descriptions lagrangienne et eulérienne du champ des vitesses dans un fluide ; savoir distinguer les définitions d’une ligne de courant et de la trajectoire d’une particule (qui ne sont confondues qu’en régime stationnaire).
● connaître les définitions du vecteur densité de courant de masse \overrightarrow{J_m}=\rho \overrightarrow{v} ; connaître et savoir retrouver l’équation locale de conservation de la masse.
● exploiter la conservation du débit massique le long d’un tube de courant en régime stationnaire.
● exploiter la conservation du débit volumique le long d’un tube de courant pour un fluide incompressible en régime quelconque, ainsi que l’équation locale \text{div}\overrightarrow{v}=0 .
Dynamique des fluides
●savoir définir la viscosité dynamique dans le cas d’un écoulement cisaillé du type \overrightarrow{v}=v_x (y,t)\overrightarrow{e_x} d’un fluide newtonien ; connaître quelques ordres de grandeur de h.
● connaître l’interprétation microscopique de la viscosité.
● connaître les conditions aux limites pour un écoulement de fluide visqueux (adhérence aux parois solides).
● interpréter le nombre de Reynolds comme le rapport d’un temps caractéristique de diffusion de quantité de mouvement sur un temps caractéristique de convection. Évaluer le nombre de Reynolds et l’utiliser pour caractériser le régime d’écoulement.
● pour les écoulements externes, connaître la notion de couche limite, la définition de la traînée et de la portance, la courbe C_x =f(Re) en échelles logarithmiques.
●pour les écoulements internes, connaître la notion de vitesse débitante, la loi de Hagen-Poiseuille et la notion de résistance hydraulique. Savoir démontrer la loi de Hagen-Poiseuille dans le cas d’une conduite circulaire à bas nombre de Reynolds, et savoir exploiter le diagramme de Moody dans le cas général.
Diffusion thermique
●connaître les trois modes de transferts thermiques, les définitions des vecteurs densité de courants thermiques associés, leur unité, leur signification, la loi de Fourier pour les échanges diffusifs et celle de Newton pour les échanges conducto-convectifs ; connaître des ordres de grandeur de la conductivité thermique de quelques matériaux.
●savoir effectuer un bilan d’énergie à 1D et 3D avec ou sans terme de production, afin d’établir une équation « de la chaleur », équation aux dérivées partielles régissant T(M,t).
●savoir exprimer les conditions aux limites dans diverses situations ; utiliser la continuité du flux thermique.
●savoir effectuer une analogie avec l’électrocinétique en régime stationnaire et dans l’A.R.Q.S. Connaître la définition de la résistance d’une conducteur thermique et son expression pour un cylindre calorifugé sur sa surface latérale.
●savoir trouver par analyse dimensionnelle l’épaisseur de peau pour les ondes thermiques ; savoir résoudre l’équation de la chaleur en régime sinusoïdal forcé.
Diffusion de particules
● connaître les deux modes de transferts de particules (diffusion et convection), les définitions des vecteurs densité de courants de particules associés, leur unité, leur signification, la loi de Fick pour les échanges diffusifs.
● savoir effectuer un bilan de particules à 1D et 3D avec ou sans terme de production, afin d’établir une équation aux dérivées partielles régissant n^\star (M,t) .
F.A.Q
\overrightarrow{\text{grad}}p est une fonction du point : les dérivées partielles spatiales comme \frac{\partial p}{\partial x}(x,y,z) sont calculées au point M(x,y,z).
On ne peut utiliser l’expression -\overrightarrow{\text{grad}}p que pour calculer la force de pression qui s’exerce sur un volume élémentaire \text{d}^3 V (du troisième ordre) au voisinage du point M(x,y,z) :
\text{d}^3 \overrightarrow{F_p}=-\overrightarrow{\text{grad}}p \; \text{d}^3 V.
Pour obtenir la force de pression sur un système dont le volume est fini dans au moins une direction, on doit donc découper ce volume et intégrer :
\overrightarrow{F_p}=-\iiint_V\overrightarrow{\text{grad}}p \; \text{d}^3 V, mais dans ce cas on utilise plutôt :
\overrightarrow{F_p}=-\oiint_{S(V)} p(M) \text{d}^2\overrightarrow{ S}, où S(V) est la surface fermée entourant le volume V.
Si la pression du fluide à la surface d’un corps est uniforme, la résultante des actions de pression est nulle.
On peut imaginer qu’au lieu du corps qui se trouve à l’intérieur de S , c’est le fluide lui-même à la pression p_0 . La force de pression qu’il subit de la part du fluide extérieur est la même que le corps puisque la pression sur sa surface est la même, sauf que dans le cas du fluide, on peut écrire la résultante sous la forme :
\overrightarrow{F_p}=-\iiint_V\overrightarrow{\text{grad}}p \; \text{d}^3 V=\overrightarrow{0} car en chaque point du volume V à l’intérieur de S, on a \overrightarrow{\text{grad}}p=\overrightarrow{0}.
Un fluide incompressible est un fluide dont le volume est indépendant de la température et de la pression (on devrait dire indilatable et incompressible) : \rho (\cancel{p},\cancel{T}).
Ce n’est jamais exactement le cas, mais c’est bien réalisé, dans le cas d’un liquide, pour des transformations usuelles. Ainsi, le modèle du fluide incompressible convient bien pour un liquide dont la profondeur est de plusieurs kilomètres.
Pour un gaz, cette hypothèse n’est pas tenable à des altitudes de l’ordre du km. Il faut donc prendre en compte le fait que \rho dépend de p et de T. Pour un gaz parfait de masse molaire M, on a \rho=\frac{Mp}{RT}, et on obtient, en appliquant la loi de la statique des fluides à l’atmosphère isotherme : p(z)=p(z=0) e^{-\frac{Mgz}{RT}} .
L’atmosphère a beau être compressible, on retrouve la loi de la statique des fluides incompressibles p(z)=p(z=0)-\rho(z=0) gz si on effectue un développement limité de p(z) quand z<<H=\frac{RT}{Mg}\simeq 8 \; \text{km} .
Le caractère incompressible ou pas d’un fluide dépend des conditions expérimentales.
Un écoulement est incompressible si une particule fluide (système fermé de masse constante) conserve son volume lors de son déplacement. Pour la particule, on a donc \rho_{\text{LAG}}(\cancel{t}). Ici \rho_{\text{LAG}}(t) est la masse volumique de la particule que l’on suit dans son déplacement (description lagrangienne). Pour un écoulement incompressible, on a donc \frac{\text{d}\rho}{\text{d}t}=0 , soit \frac{\partial\rho}{\partial t} +\overrightarrow{v}\cdot\overrightarrow{\text{grad}}\rho =0, en utilisant la formule de dérivation particulaire.
Un écoulement de liquide pourra généralement être considéré comme incompressible, mais un écoulement de gaz également, sous certaines restrictions. Ainsi, un écoulement de gaz largement subsonique (à des vitesses petites devant la vitesse du son dans ce gaz) peut être considéré comme incompressible.
La poussée d’Archimède est la résultante des actions de pression qu’exerce un fluide, ou un ensemble de fluides, sur un corps, lorsque le fluide et le corps sont au repos dans un référentiel galiléen.
Lorsque le corps est en mouvement dans le fluide, il met également en mouvement le fluide autour de lui. Il y a donc un écoulement. Dans ce cas, le champ de pression du fluide en contact avec le corps n’est plus celui de la statique. Il faut rajouter le champ de pression dynamique dû à l’écoulement, c’est à dire les forces de traînée et de portance.
Dans le cas où la masse volumique du corps est très grande devant celle du fluide, on peut négliger la poussée d’Archimède. Ainsi, un avion, contrairement à une montgolfière ou un dirigeable, ne vole pas parce qu’il est plus léger que l’air (il ne l’est pas…) mais parce qu’il se déplace rapidement dans l’air et qu’il est soumis à une force de portance.
Oui, car si la particule, qui se déplace selon une ligne de courant pour un écoulement stationnaire, rencontre un champ de pression qui n’est pas uniforme, la pression de cette particule varie dans le temps : p_{\text{LAG}}(t)=p_{\text{EUL}}(M(t),\cancel{t}), soit, en utilisant la formule de dérivation particulaire :
\frac{\text{d}p}{\text{d}t}=\underset{=0}{\frac{\partial p}{\partial t}}+\underset{\ne 0}{\overrightarrow{v}\cdot\overrightarrow{\text{grad}}p}\ne 0.
Ces notions sont définies dans un référentiel donné.
Une ligne de courant est définie à un instant donné t . C’est une ligne telle qu’en chacun de ses points M le vecteur vitesse \overrightarrow{v}_{\text{EUL}}(M,t) soit tangent à la ligne. Un déplacement élémentaire \text{d}\overrightarrow{OM} le long de la ligne est donc tel que \overrightarrow{v}_{\text{EUL}}(M,t) \wedge \text{d}\overrightarrow{OM} =\overrightarrow{0}.
Pour un écoulement instationnaire, les lignes de courants changent à chaque instant.
La trajectoire d’une particule est la suite des positions occupées par la particule au cours du temps. On peut la trouver à partir du champ des vitesses en écrivant que la vitesse de la particule à la date t est égale à la vitesse à la date t au point M(t) où se trouve la particule :
\frac{\text{d}\overrightarrow{OM}}{\text{d}t}=\overrightarrow{v}_{\text{EUL}}(M(t),t) .
La description eulérienne est la description « naturelle » d’un écoulement à l’aide de champs : champ de vitesse, champ de pression, de masse volumique, etc. Elle se prête bien à l’écriture des conditions aux limites (par exemple : champ de vitesse nul à la surface d’un obstacle solide).
L’équation locale de conservation de la masse \frac{\partial\rho}{\partial t} +\text{div}(\rho\overrightarrow{v})=0 s’obtient sans problème en description eulérienne : pas besoin de se ramener à un système fermé, on effectue un bilan de masse au système ouvert situé à l’intérieur d’une surface fermée fixe dans le référentiel d’étude.
En revanche, pour appliquer le principe fondamentale de la dynamique, il faut nécessairement étudier un système fermé, soit une particule fluide que l’on suit dans son déplacement entre t et t+\text{d}t (description lagrangienne). On utilise donc, très momentanément, la description lagrangienne, puisque la formule de dérivation particulaire \frac{\text{d}\overrightarrow{v}}{\text{d}t}=\frac{\partial \overrightarrow{v}}{\partial t}+\left(\overrightarrow{v}\cdot\overrightarrow{\text{grad}}\right)\overrightarrow{v} permet de relier l’accélération de la particule au champ de vitesse.
Notons au passage que, pour un écoulement incompressible, les deux équations {équation locale de conservation de la masse, principe fondamental appliqué à une particule fluide} suffisent, lorsque les conditions aux limites sont connues, pour déterminer le champ de vitesse et de pression.
Un système fluide étudié dans un référentiel galiléen (et donc une particule fluide, qui est un tel système, mais contenu dans un volume élémentaire \text{d}^3 V : du troisième ordre), est soumis à :
- des forces surfaciques : forces de pression et forces visqueuses ;
- des forces volumiques, le plus souvent : uniquement le poids du système.
Dans le cas d’une particule fluide, la résultante des actions de pression est \text{d}^3 \overrightarrow{F_p}=-\overrightarrow{\text{grad}}p \; \text{d}^3 V. Les forces de pression sont normales à une surface élémentaire et proportionnelles à cette surface, mais leur résultante est, elle, proportionnelle au volume \text{d}^3 V de la particule.
Le poids de la particule s’écrit \text{d}^3 \overrightarrow{P}=\rho \overrightarrow{g} \text{d}^3 V.
Enfin, la résultante des actions visqueuses s’écrit, pour un écoulement incompressible, \text{d}^3 \overrightarrow{F_\text{visq}}= \eta \Delta\overrightarrow{v}\text{d}^3 V. Là encore, la résultante des actions visqueuses, qui possèdent des composantes tangentielles à une surface élémentaire, et sont proportionnelles à cette surface, est proportionnelle au volume de la particule. Cette expression n’est pas au programme en PSI, mais elle peut être fournie dans un énoncé de concours, ou bien l’expression du P.F.D appliqué à une particule fluide dans un référentiel galiléen, appelée équation de Navier et Stokes :
\rho\left[\frac{\partial \overrightarrow{v}}{\partial t}+\left(\overrightarrow{v}\cdot\overrightarrow{\text{grad}}\right)\overrightarrow{v}\right]=-\overrightarrow{\text{grad}}p+\rho \overrightarrow{g} +\eta \Delta\overrightarrow{v}
Prenons l’exemple d’un écoulement de Couette où le champ de vitesse est de la forme \overrightarrow{v}=v_x(y,t)\overrightarrow{e_x}, avec v_x(y,t)\ge 0 fonction croissante de y.
Les particules fluides se déplacent selon \overrightarrow{e_x} et « charrient » avec elles de la masse, de l’énergie cinétique, de la quantité de mouvement. Ce mouvement étant macroscopique, on parle de transport convectif de quantité de mouvement.
Cependant, même si, en moyenne, les molécules se déplacent selon \overrightarrow{e_x}, elles ont une composante aléatoire de vitesse non nulle selon \overrightarrow{e_y}. Celles qui se déplacent selon +\overrightarrow{e_y} emmènent donc une quantité de mouvement selon \overrightarrow{e_x} inférieure à celle qu’emmènent celles qui se déplacent selon -\overrightarrow{e_y}. Il en résulte qu’une particule fluide en y est « accélérée » par sa voisine en y+\text{d}y (et « freinée » par sa voisine en y-\text{d}y). Ce transport de quantité de mouvement, qualifié de diffusif car lié au déplacement microscopique du fluide, est donc à l’origine des forces visqueuses.
Considérons l’écoulement de débit volumique q_V dans une conduite circulaire d’axe Oz. La vitesse n’est pas uniforme dans une section droite (d’équation z=Cte). Le « profil » de vitesse dépend du nombre de Reynolds. Il est parabolique pour Re<2000 : écoulement laminaire parallèle à Oz, et quasiment uniforme en moyenne temporelle (sauf très près des parois sur lesquelles il s’annule) pour Re>3000 : écoulement turbulent.
Dans tous les cas, la vitesse débitante u est une vitesse moyenne, celle correspondant à un écoulement uniforme de même débit : si S est l’aire de la section de la conduite, on a q_V=S\cdot u.
Une couche limite apparaît pour un écoulement de fluide autour d’un obstacle à grand nombre de Reynolds (Re>2000). Cette couche est alors très fine (de quelques micromètres à quelques millimètres) et correspond à la zone de l’écoulement proche de l’obstacle pour laquelle la viscosité ne peut pas être négligée (la vitesse, qui s’annule à la surface de l’obstacle, subit un fort gradient transversal dans cette couche; on parle de cisaillement, et l’écoulement y est tourbillonnaire). En revanche, hors de la couche limite, l’écoulement peut être considéré comme parfait et irrotationnel. Selon le profil de l’obstacle, la couche limite « décolle » plus où moins en aval (très en aval pour un solide bien profilé) et délimite le sillage turbulent où la viscosité ne peut pas non plus être négligée puisque l’écoulement y est très tourbillonnaire.
Même pour un corps bien profilé, la couche limite doit être prise en compte car :
- les conditions aux limites ne sont pas les mêmes si elle est présente (adhérence du fluide à la paroi) que pour un fluide parfait partout (seule la vitesse normale du fluide sur la paroi serait nulle);
- En l’absence de viscosité, il n’y aurait pas de force de traînée (et on peut montrer qu’il n’y aurait pas non plus de force de portance) pour un écoulement de fluide stationnaire autour d’un obstacle.
Pour un écoulement à plus faible nombre de Reynolds, la zone où l’écoulement est « visqueux » est grande et on ne parle pas de couche limite (pour un écoulement autour d’une sphère à Re<1, la zone visqueuse s’étend sur plusieurs dizaines de rayons de la sphère…).
Transport de charges (conduction électrique) : \overrightarrow{J}=\sum{\rho_i \overrightarrow{v}_i} en \text{C}\cdot\text{s}^{-1}\cdot\text{m}^{-2}=\text{A}\cdot\text{m}^{-2} , qui permet de calculer l’intensité algébrique du courant traversant une surface orientée :
I=\frac{\delta q}{\text{d}t}=\iint_{S} \overrightarrow{J} \cdot \text{d}^2\overrightarrow{ S}.
Une surface élémentaire \text{d}^2 S est traversée pendant \text{d}t par une charge \delta^3 q= \overrightarrow{J} \cdot \text{d}^2\overrightarrow{ S} \text{d}t.
Transport de masse : \overrightarrow{J_m}=\rho \overrightarrow{v} en \text{kg}\cdot\text{s}^{-1}\cdot\text{m}^{-2} , qui permet de calculer le débit massique traversant une surface orientée :
q_{\text{m}}=\frac{\delta m}{\text{d}t}=\iint_{S} \overrightarrow{J_m} \cdot \text{d}^2\overrightarrow{ S}.
Une surface élémentaire \text{d}^2 S est traversée pendant \text{d}t par une masse \delta^3 m= \overrightarrow{J_m} \cdot \text{d}^2\overrightarrow{ S} \text{d}t.
Transport d’énergie cinétique (conduction, ou diffusion thermique) : \overrightarrow{J}_{\text{d}} en \text{J}\cdot\text{s}^{-1}\cdot\text{m}^{-2}=\text{W}\cdot\text{m}^{-2} , qui permet de calculer la puissance thermique algébrique traversant une surface orientée :
P_{\text{th}}=\Phi= \frac{\delta Q}{\text{d}t}=\iint_{S} \overrightarrow{J}_{\text{d}} \cdot \text{d}^2\overrightarrow{ S}.
Une surface élémentaire \text{d}^2 S est traversée pendant \text{d}t par une énergie : chaleur \delta^3 Q= \overrightarrow{J}_{\text{d}} \cdot \text{d}^2\overrightarrow{ S} \text{d}t.
Transport de particules (diffusion de particules) : \overrightarrow{J}_{\text{d}} en \text{s}^{-1}\cdot\text{m}^{-2} , qui permet de calculer le nombre de particules (algébrique) traversant par unité de temps une surface orientée :
\frac{\delta N}{\text{d}t}=\iint_{S} \overrightarrow{J}_{\text{d}} \cdot \text{d}^2\overrightarrow{ S}.
Une surface élémentaire \text{d}^2 S est traversée pendant \text{d}t par un nombre de particules \delta^3 N= \overrightarrow{J}_{\text{d}} \cdot \text{d}^2\overrightarrow{ S} \text{d}t.
