Réflexion d’une O.P.P dans un milieu non dispersif
Réflexion d’une O.P.P.H
Une O.P.P.H qui se propage selon les x croissants est réfléchie en x=0 (à droite sur les figures ci-dessous) avec un coefficient de réflexion réel r.
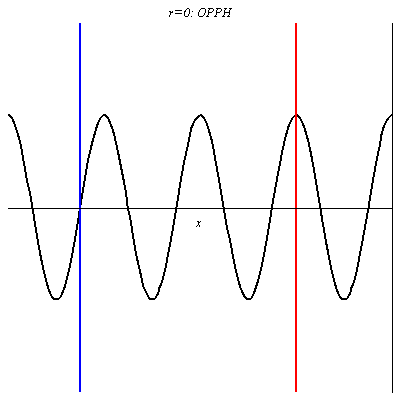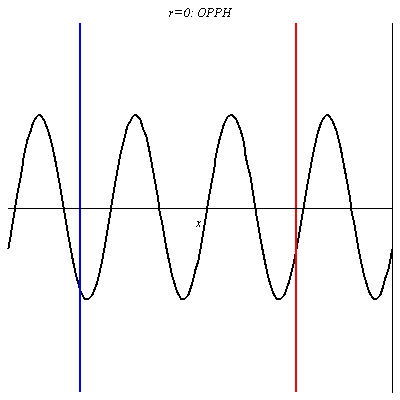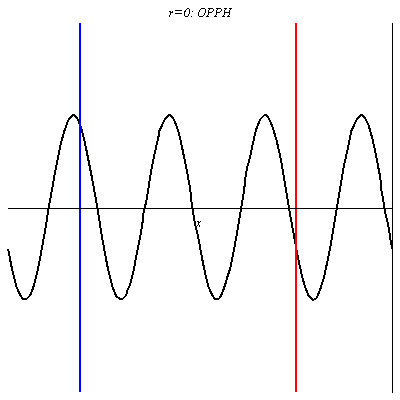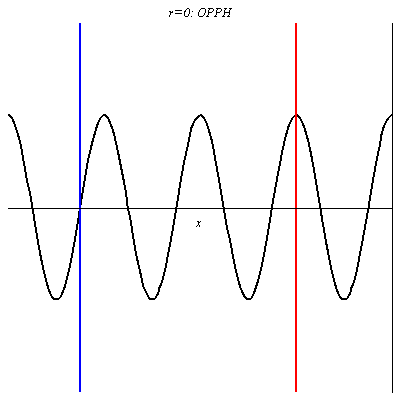
Pour r = 0, il n’y a pas d’onde réfléchie donc l’onde résultante est l’O.P.P.H incidente.
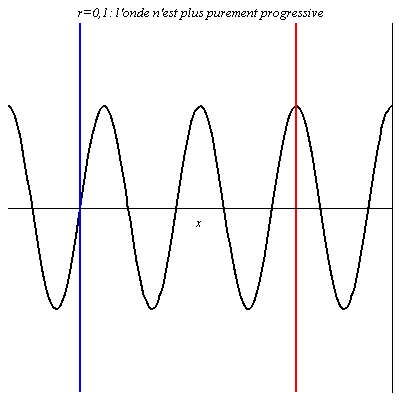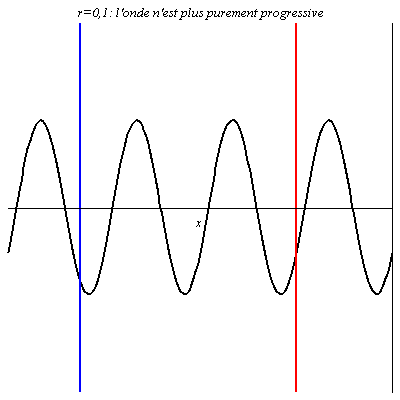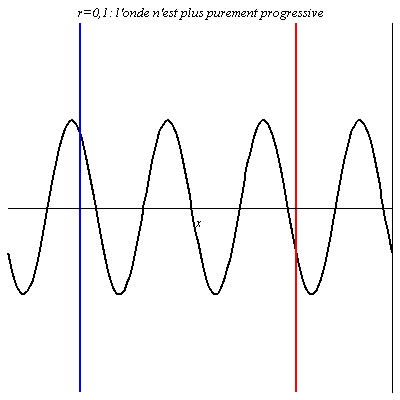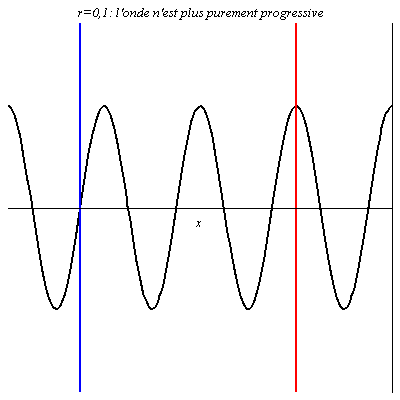

Pour r = 0,1, l’onde réfléchie est en phase en certains points avec l’onde incidente (ventres de vibration comme au niveau du trait rouge), et en opposition de phase en d’autres points (nœuds de vibration comme au niveau du trait bleu). Néanmoins, en ces derniers points, l’onde résultante n’est pas nulle car les deux ondes n’ont pas la même amplitude : l’amplitude de vibration y est juste plus petite qu’ailleurs. L’onde résultante progresse dans le sens des x croissants mais n’est plus purement progressive.
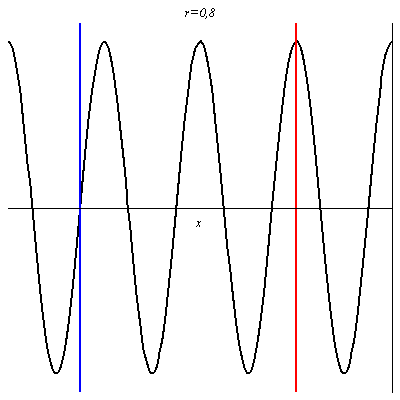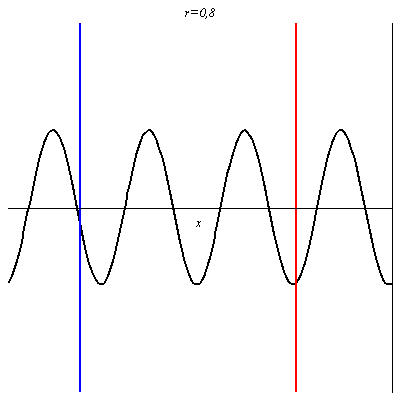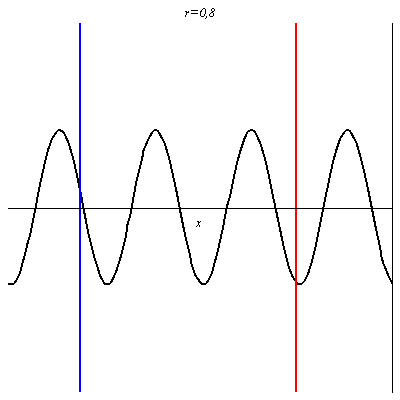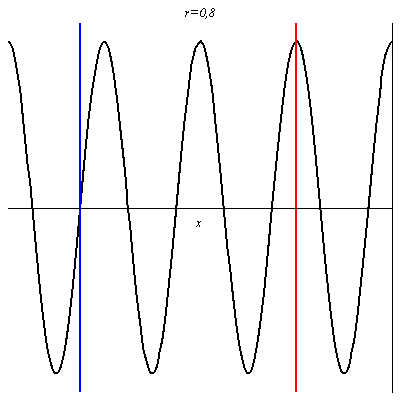
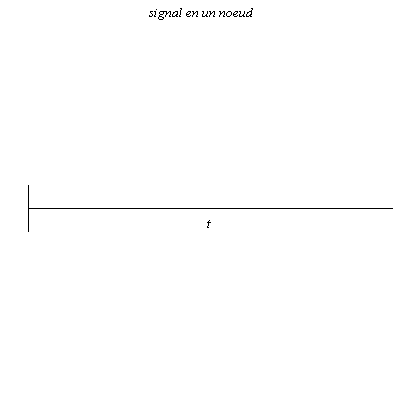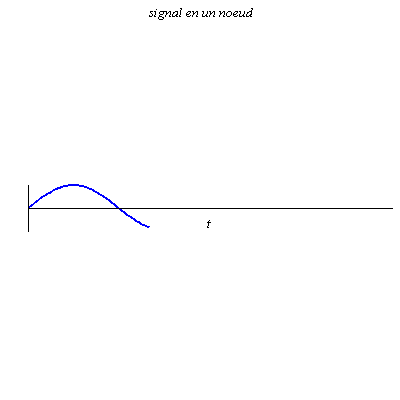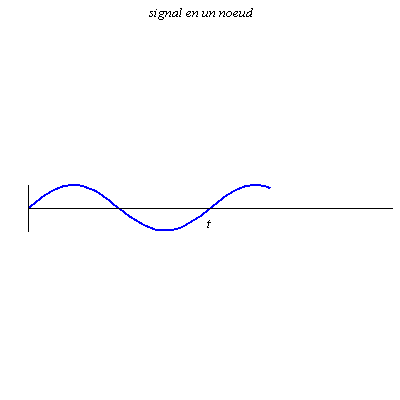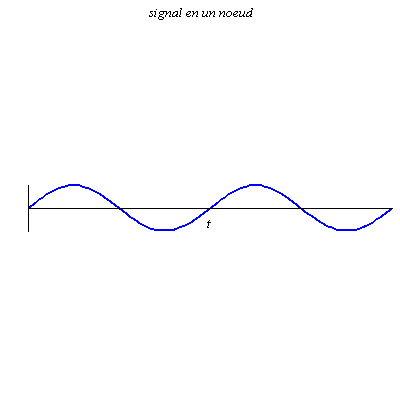

Pour r = 0,8, le contraste (différence d’amplitude entre les ventres et les nœuds) est plus grand, mais l’onde résultante progresse encore dans le sens des x croissants.
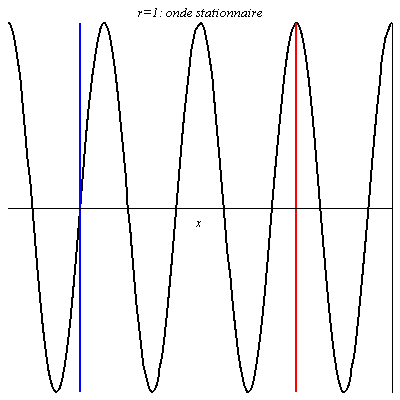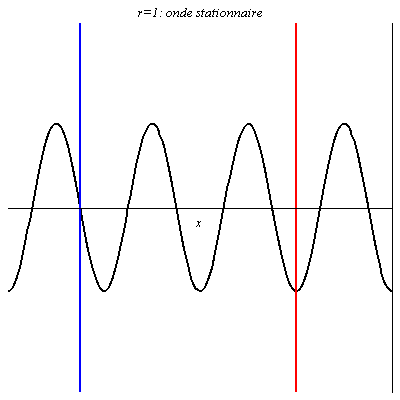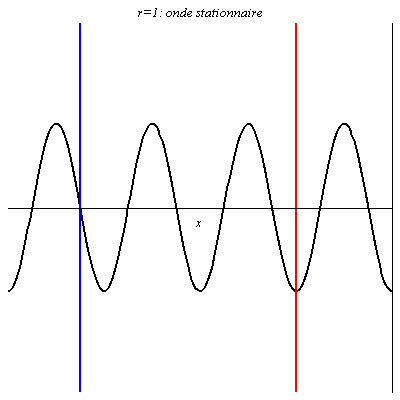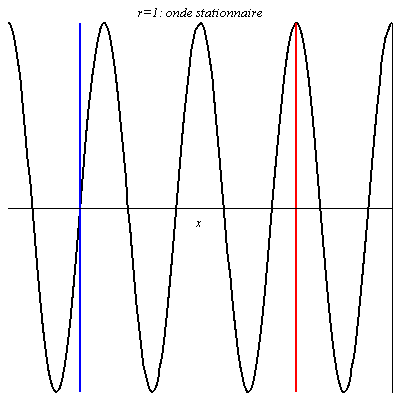
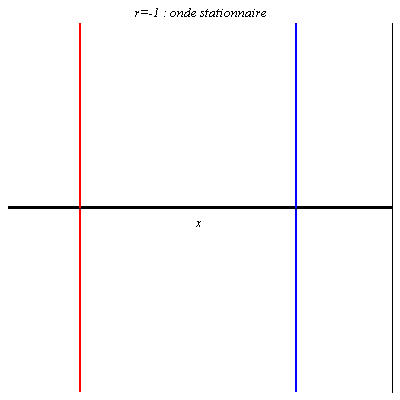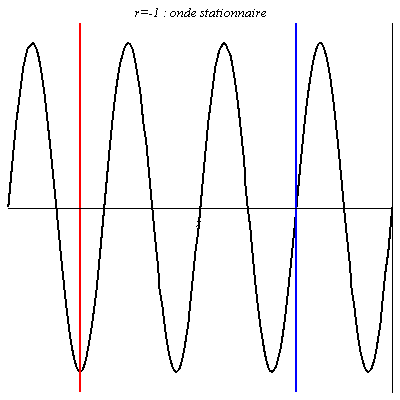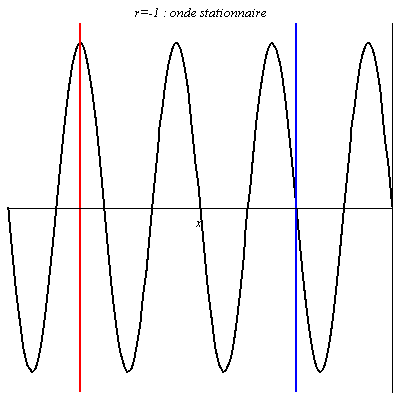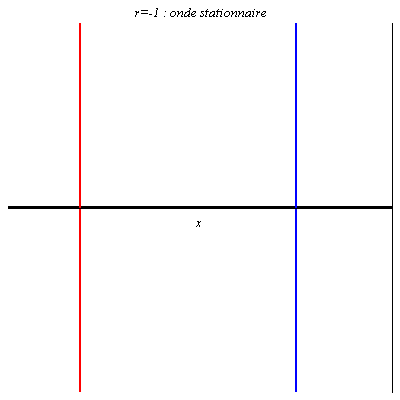

Pour r = 1 ou r = -1, l’onde résultante, obtenue par interférences entre l’onde réfléchie et l’onde incidente, est stationnaire (l’amplitude de la vibration est nulle pour les nœuds). La seule différence est un décalage entre les positions des nœuds et des ventres (on a en x=0 un ventre pour r = 1, et un nœud pour r = -1).
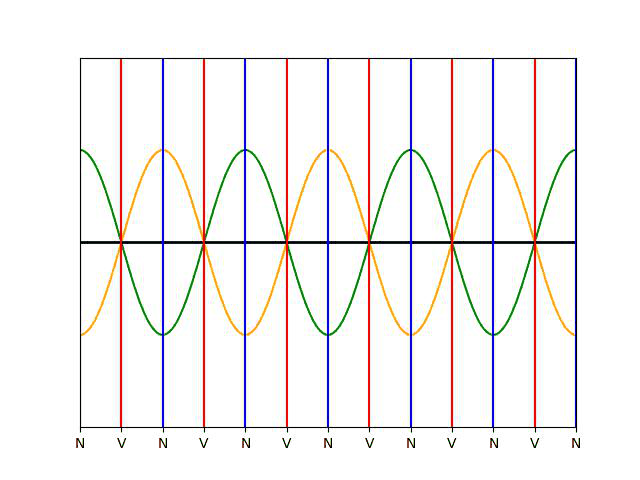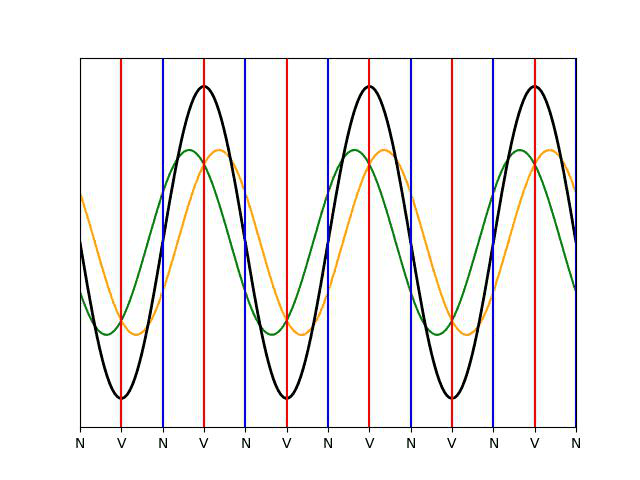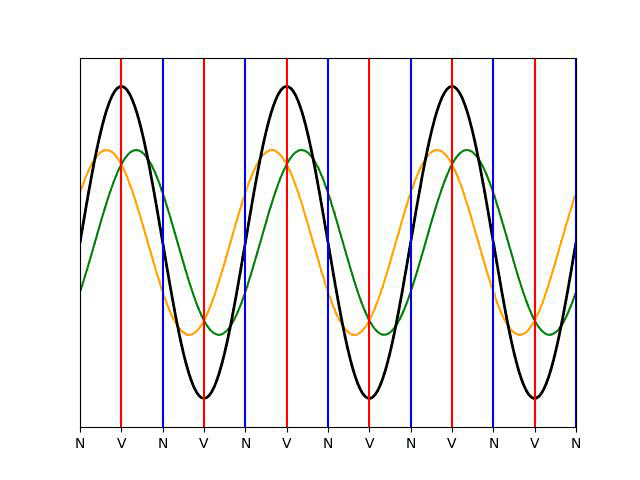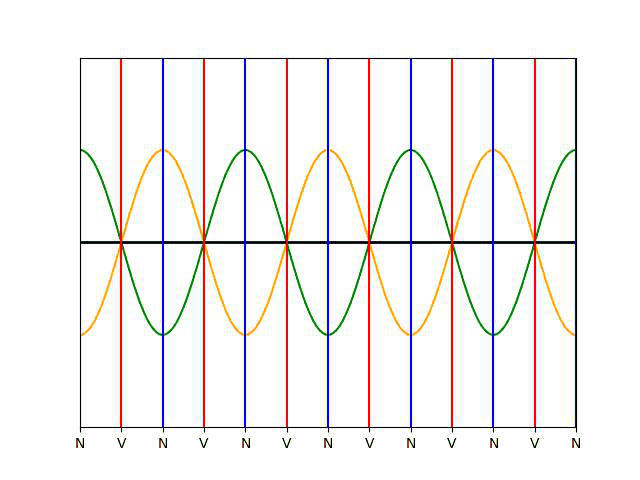
L’onde stationnaire (en noir) se décompose en une onde incidente (en vert, qui va de gauche à droite) et en une onde réfléchie (en orange, qui va de droite à gauche), de même amplitude. Les nœuds de vibration, notés « \text{N} » , sont les points où onde incidente et réfléchie sont en opposition de phase, les ventres de vibration, notés « \text{V} » , sont les points où onde incidente et réfléchie sont en phase.
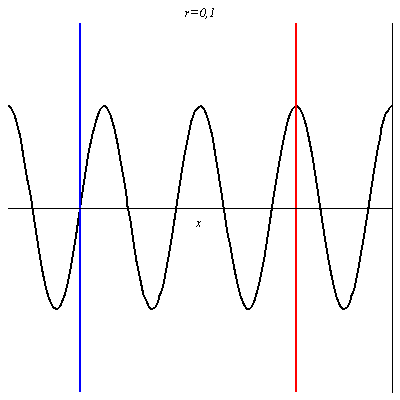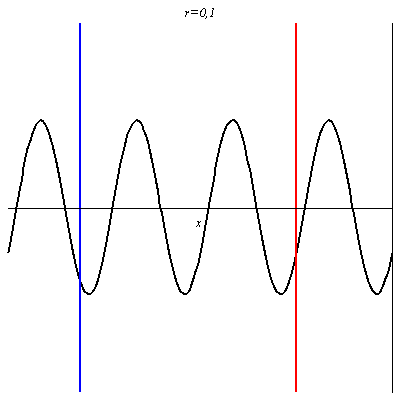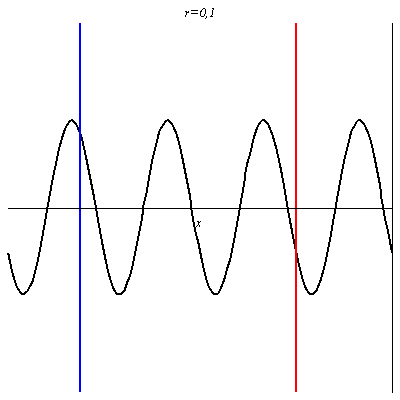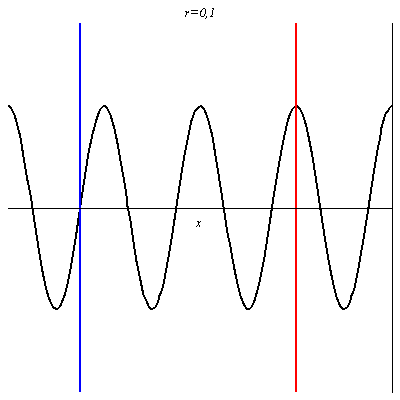
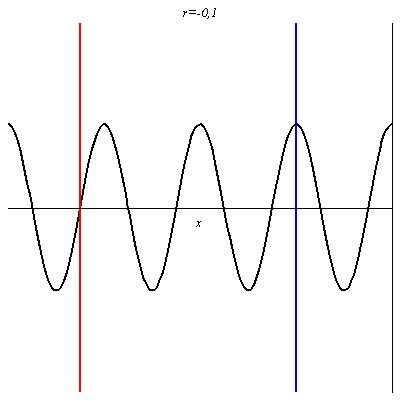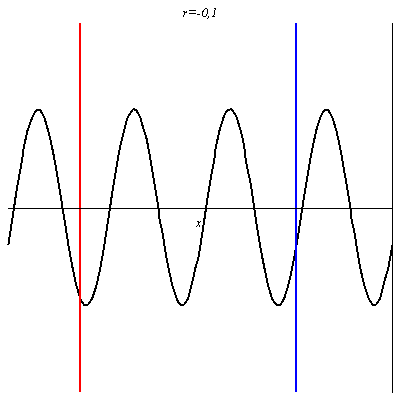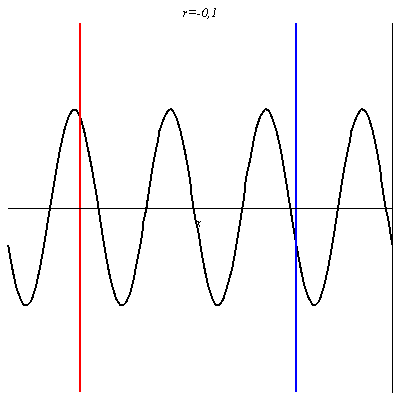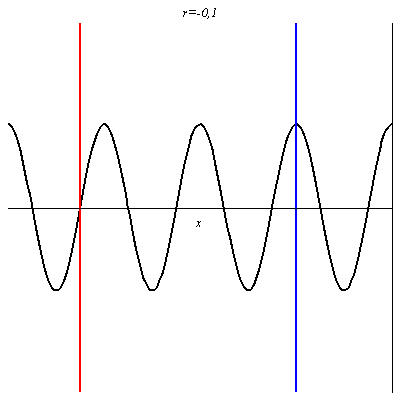

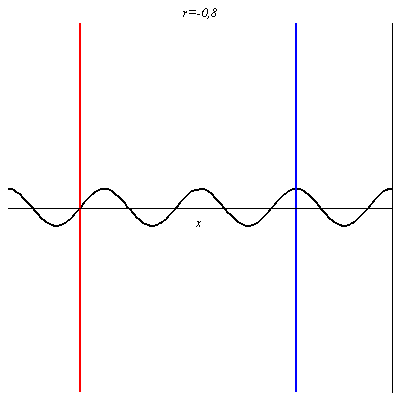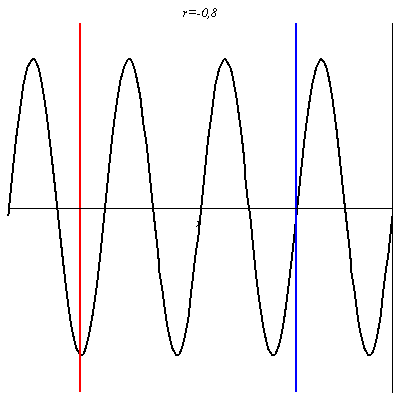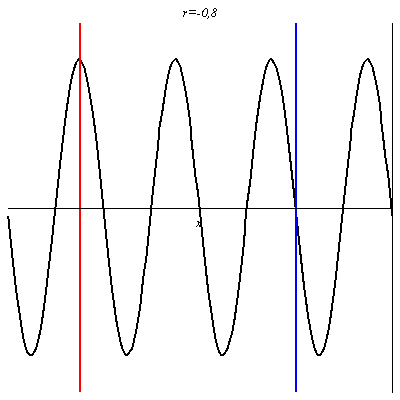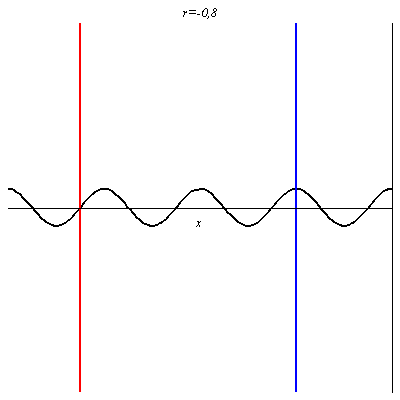
Pour -1 < r < 0 on retrouve une onde non purement progressives avec des nœuds et des ventres dont les positions sont inversés par rapport au cas où r > 0.
Réflexion d’une O.P.P quelconque (exemple du câble coaxial)
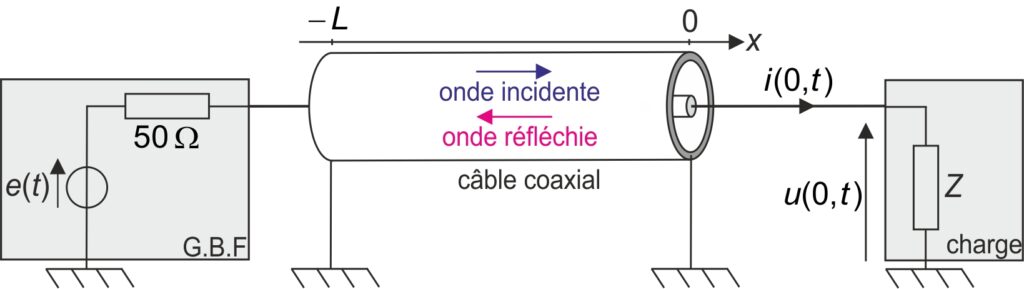
L’O.P.P incidente se propage selon les x croissants et se réfléchit en x=0 avec un coefficient de réflexion réel r.
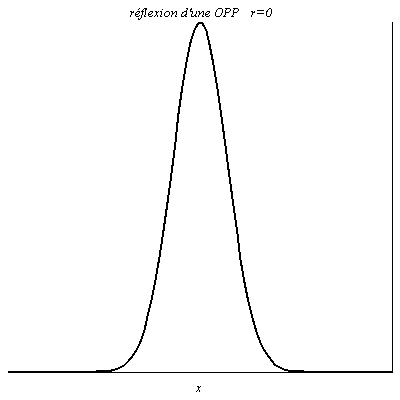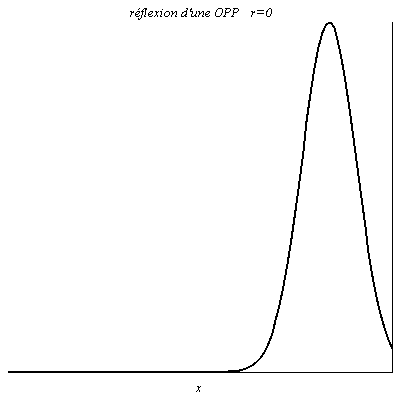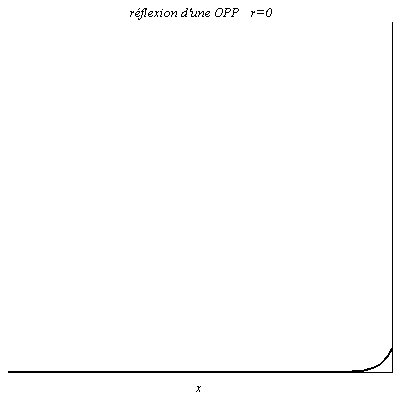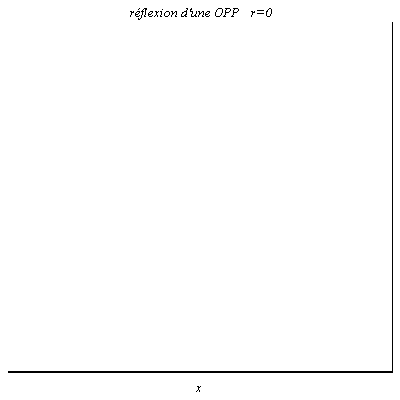
On a par exemple r=0 lorsque l’on place à l’extrémité d’un câble coaxial un conducteur ohmique de résistance égale à son impédance caractéristique. On parle d’adaptation d’impédance puisque aucune onde n’est réfléchie : toute la puissance propagée par le câble est transmise à la charge, c’est-à-dire au conducteur ohmique.
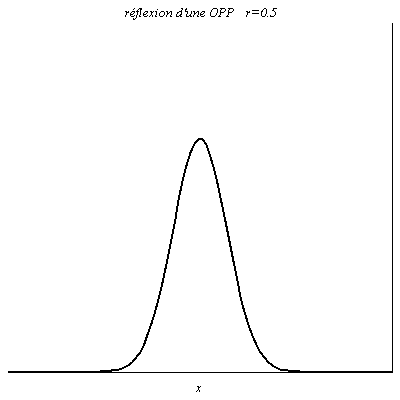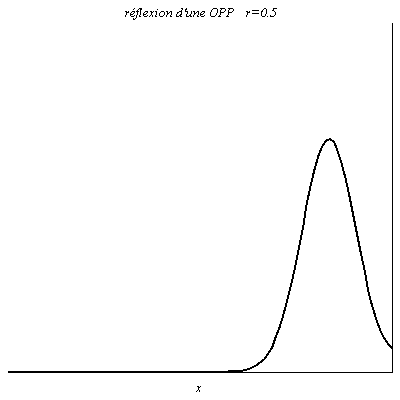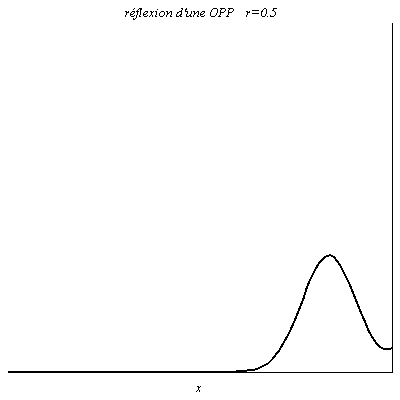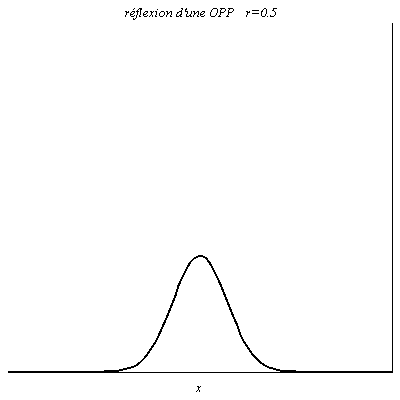
Quand r>0, l’onde réfléchie est en phase en x=0 avec l’onde incidente, avec une amplitude différente si r \ne 1. Une onde scalaire positive le reste après réflexion. On a un coefficient de réflexion r=0,5 dans le cas du câble coaxial d’impédance caractéristique Z_{\text{c}} s’il est terminé par un conducteur ohmique de résistance Z=3Z_{\text{c}} car le coefficient de réflexion en tension vaut \rho_u=\frac{Z-Z_{\text{c}}}{Z+Z_{\text{c}}}.
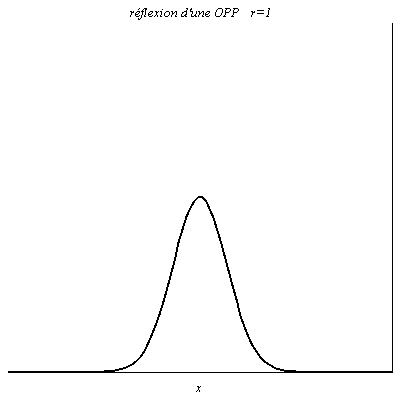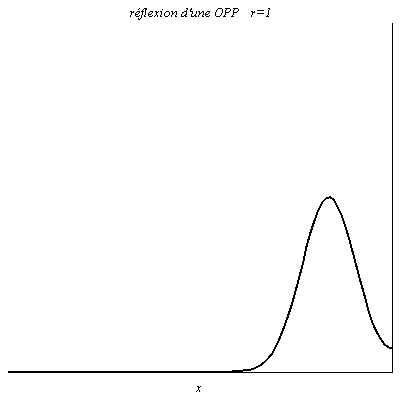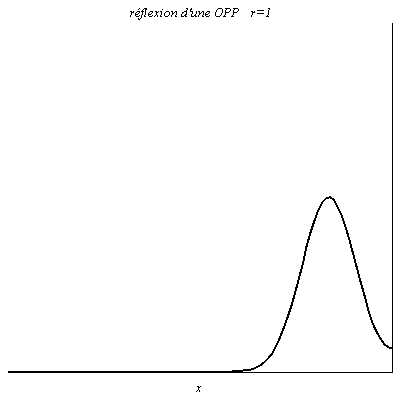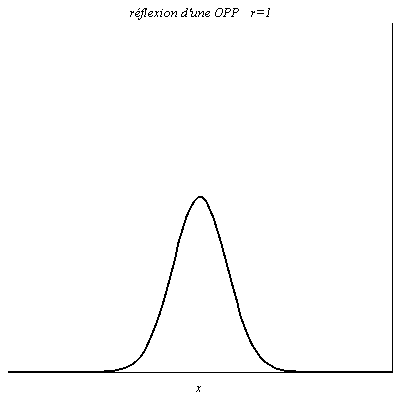
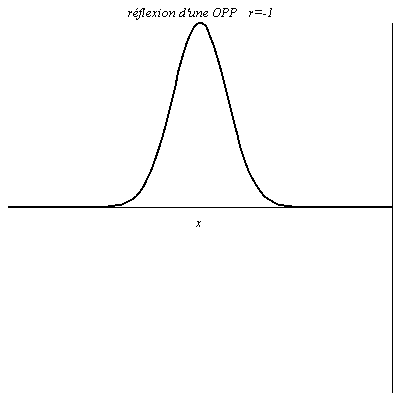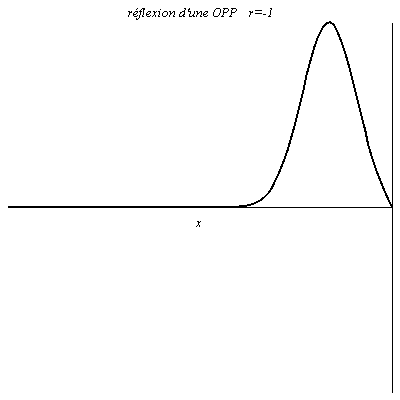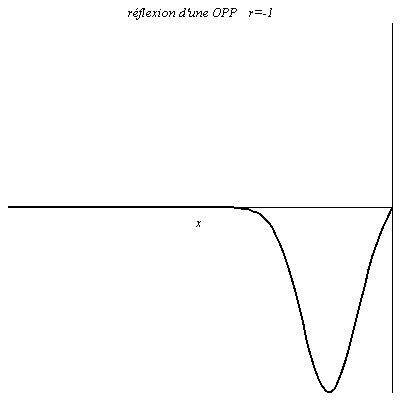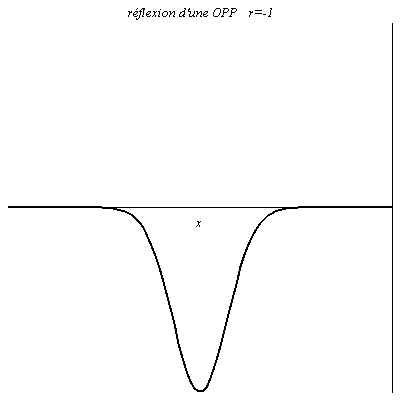
Quand r=1, à tout instant la valeur du signal réfléchie est égale à celle du signal incident en x=0 (le signal résultant y est le double du signal incident). L’onde est réfléchie sans changement de signe. C’est le cas pour la tension dans un câble coaxial ouvert à son extrémité (\rho_u\underset{Z\to +\infty}{\longrightarrow}1).
Quand r<0, l’onde réfléchie est en opposition de phase en x=0 avec l’onde incidente. Une onde scalaire positive devient négative après réflexion.
Pour r=-1, à tout instant la valeur du signal réfléchie est opposée à celle du signal incident en x=0 (le signal résultant y est nul). L’onde est réfléchie avec la même amplitude mais changement de signe. C’est le cas pour la tension dans un câble coaxial court-circuité à son extrémité (\rho_u\underset{Z\to 0}{\longrightarrow}-1). On a en effet dans ce cas imposé un nœud de tension en x=0.
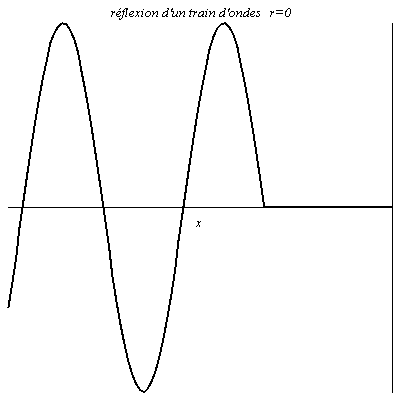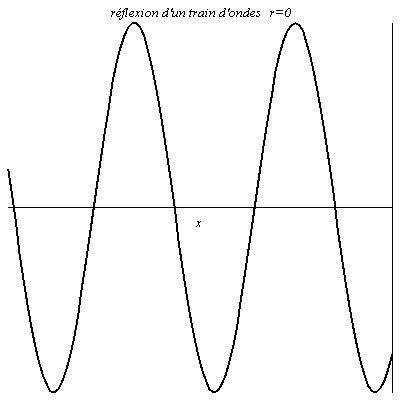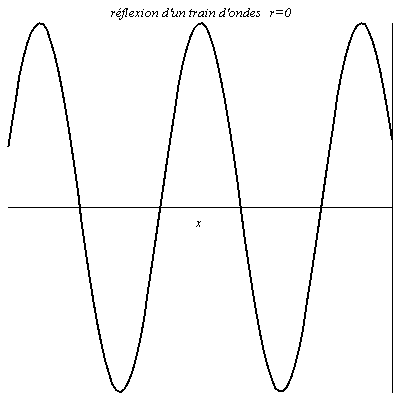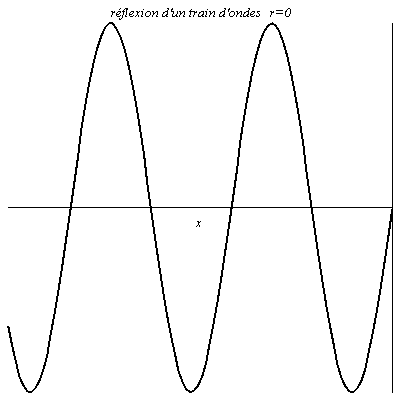
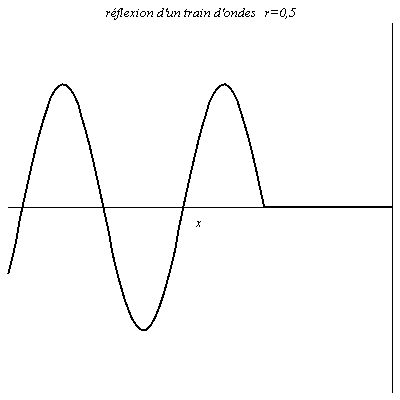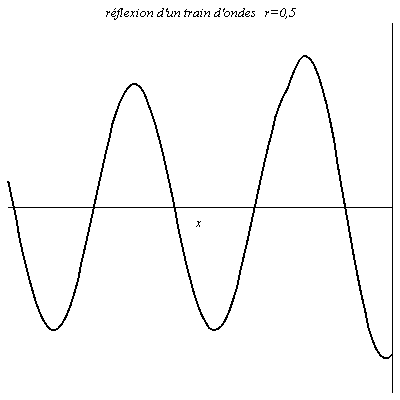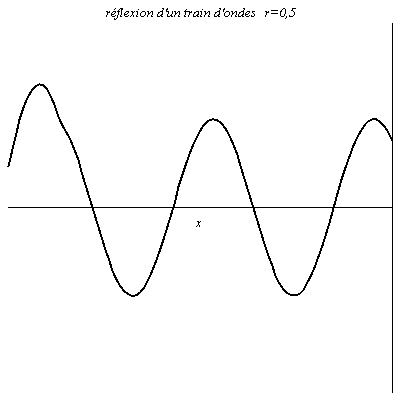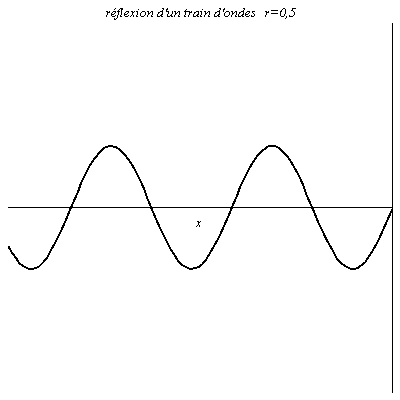
Réflexion d’un train d’onde
L’onde est sinusoïdale mais possède un début. Il y a donc un régime transitoire avant que l’on ait en chaque point de la figure une résultante de l’onde réfléchie et de l’onde incidente.
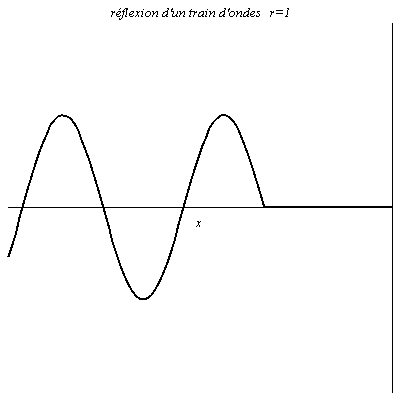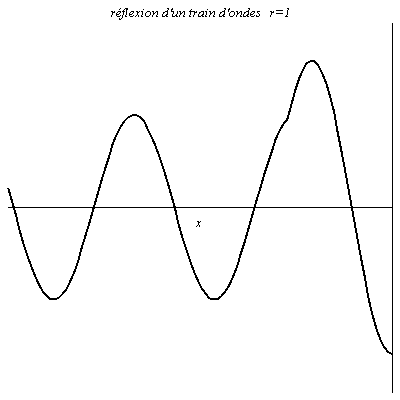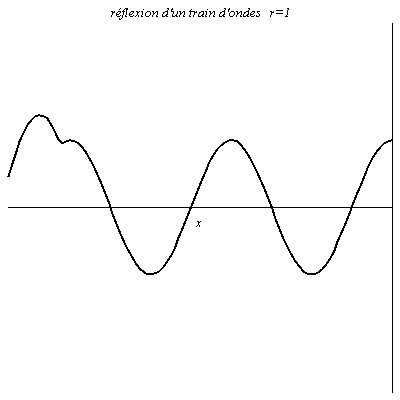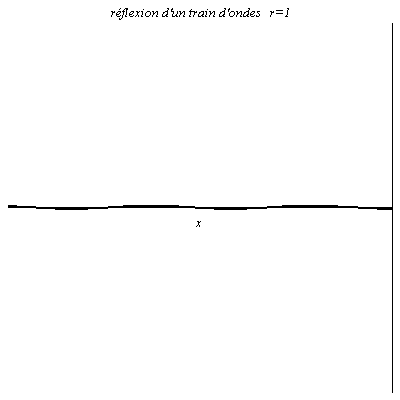
Onde le long d’une corde de guitare et de piano
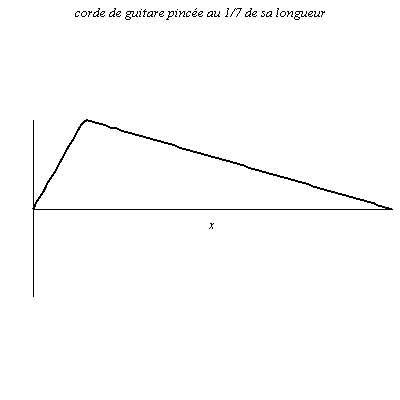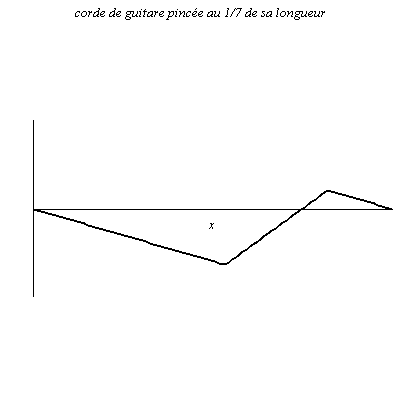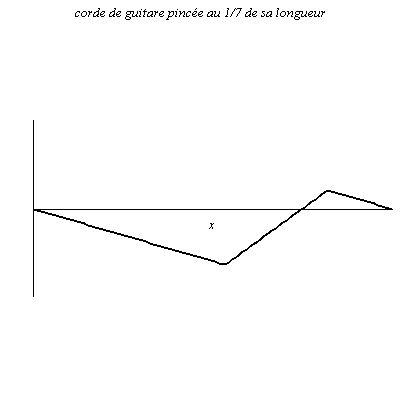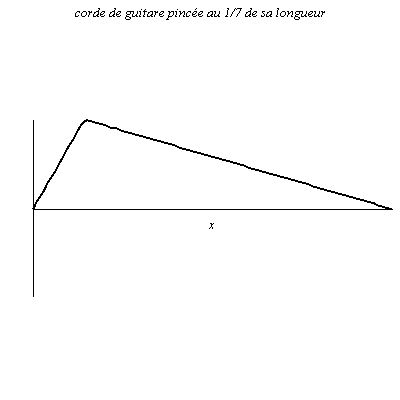
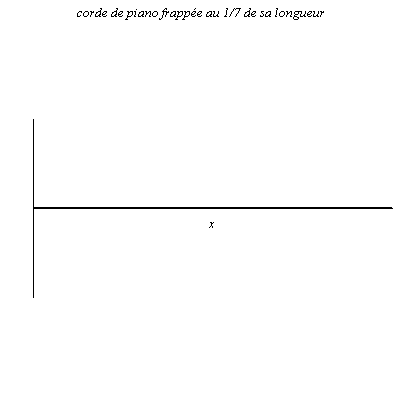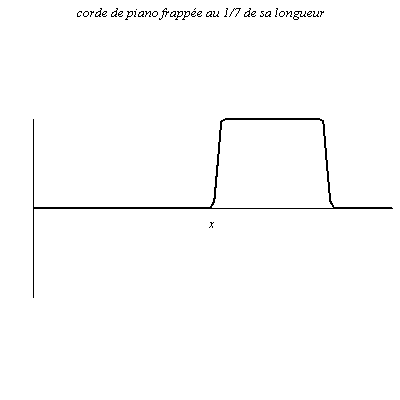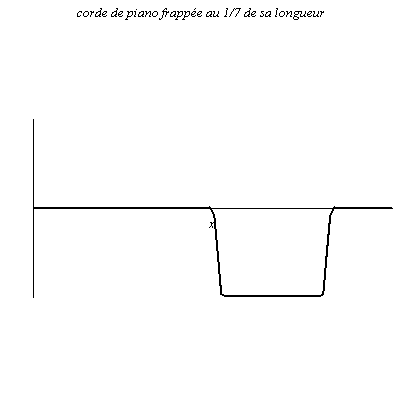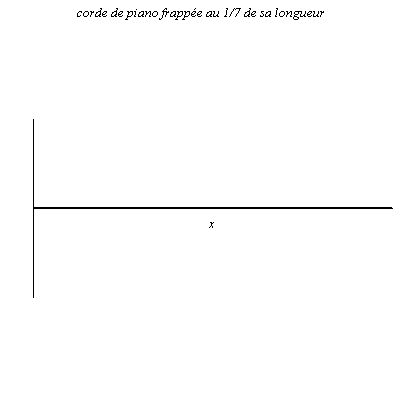
La corde de longueur L est attachée à ses deux extrémités (nœuds de vibration).
Un mode propre de vibration est un mode dans lequel la vibration temporelle est sinusoïdale (le spectre du signal temporel ne contient qu’une seule raie). Il vérifie l’équation de d’Alembert \frac{\partial^2\psi}{\partial x^2}=\frac{1}{c^2}\frac{\partial^2\psi}{\partial t^2}, et les conditions aux limites :
\psi(x=0,t)=0 \;\forall t et \psi(x=L,t)=0 \; \forall t.
La pulsation temporelle du mode propre de rang n est \omega_n=\frac{n \pi c }{L}, et sa pulsation spatiale est k_n=\frac {\omega_n}{c}=\frac{n \pi}{L}. Ce mode propre s’écrit donc sous la forme :
\psi_n (x,t)=\psi_{0n}\text{cos}\left(\frac{n \pi c t}{L}+\phi_n\right)\text{sin}\left(\frac{n \pi x}{L}\right)=\left[a_n \text{cos}\left(\frac{n \pi c t}{L}\right) +b_n \text{sin}\left(\frac{n \pi c t}{L} \right)\right]\text{sin}\left(\frac{n \pi x}{L}\right)
Si on superpose les modes propres :
\psi(x,t)=\sum\limits_{n=1}^{n=\infty}\left[ a_n \text{cos}\left(\frac{n \pi c t}{L}\right) +b_n \text{sin}\left(\frac{n \pi c t}{L} \right)\right]\text{sin}\left(\frac{n \pi x}{L}\right),
l’équation de d’Alembert, linéaire, est toujours vérifiée, ainsi que les conditions aux limites.
On vérifie enfin les conditions initiales (position initiale de la corde définie par une fonction F : \psi(x,t=0)=F(x) \;\forall x \in [0,L], et vitesse initiale de la corde définie par une fonction G : \frac{\partial \psi}{\partial t}(x,t=0)=G(x) \;\forall x \in [0,L]) en ajustant les coefficients a_n et b_n.
L’onde peut aussi être vue comme la superposition d’ondes obtenues par réflexions sur les deux extrémités de la corde.
Les animations obtenues ci-dessus sont peu réalistes car elles ne tiennent pas compte de phénomènes dissipatifs (frottement de la corde avec l’air), de la raideur de la corde, du couplage entre les cordes et le chevalet…
Ondes stationnaires sur une peau de tambour circulaire (non planes)
Les fréquences f_{mn} des modes propres d’une peau de tambour circulaire sont doublement quantifiées.
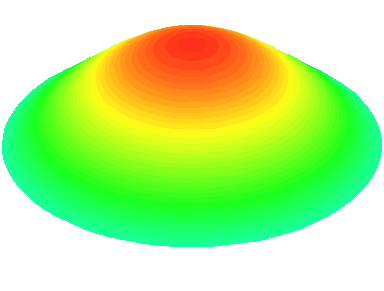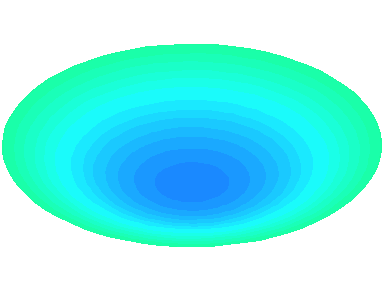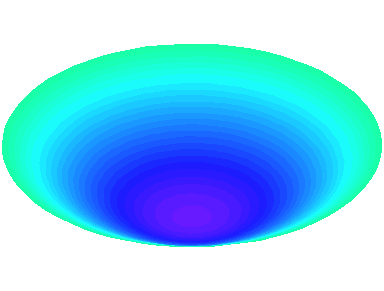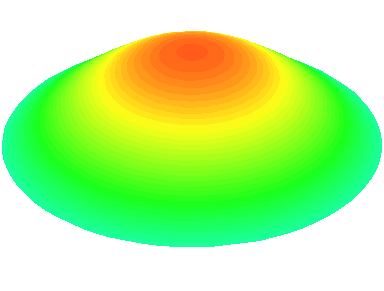
m=0 : symétrie de révolution.
n=1 : les seuls nœuds se trouvent sur le cadre circulaire de la peau.
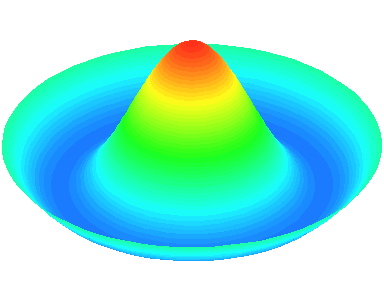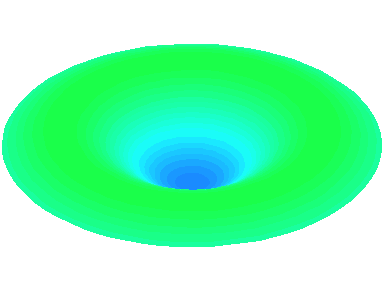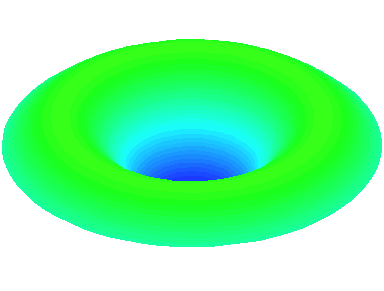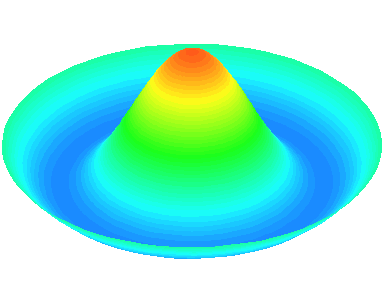
m=0.
n=2 : un autre anneau nodal apparaît.
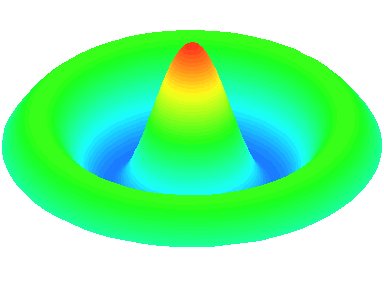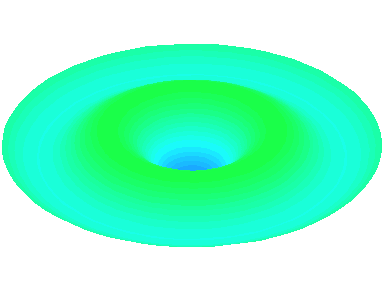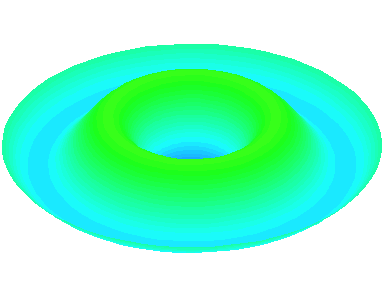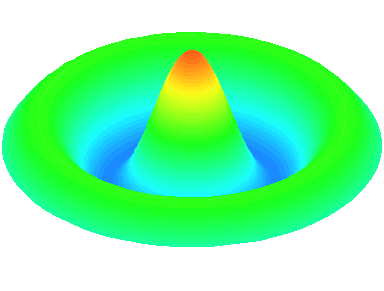
m=0.
n=3 : un troisième anneau nodal apparaît.
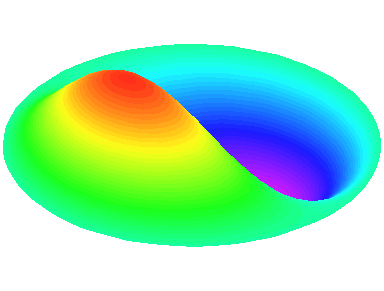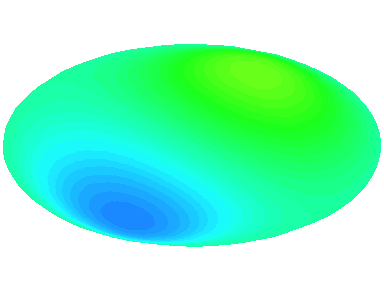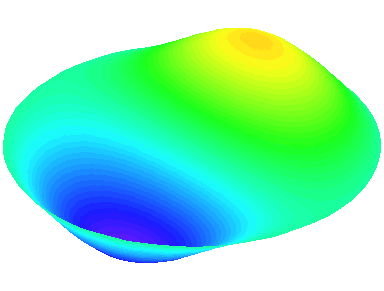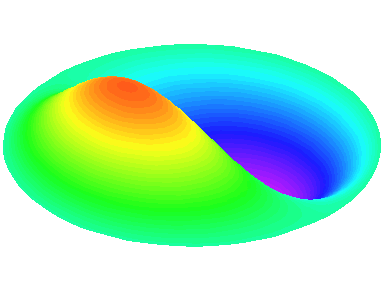
m=1 : une ligne nodale apparaît sur un diamètre \theta=0.
n=1 : les autres nœuds se trouvent sur le cadre circulaire de la peau.
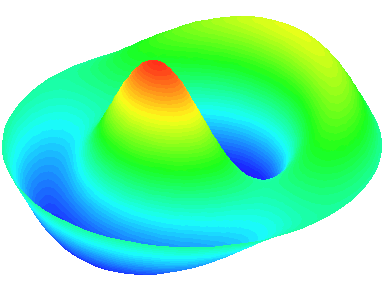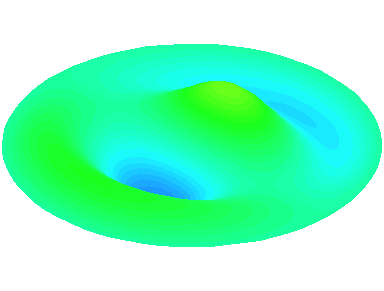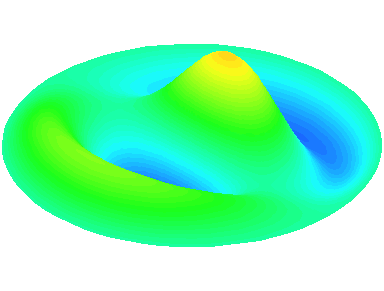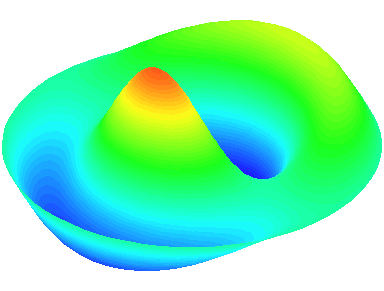
m=1.
n=2 : un autre anneau nodal apparaît.
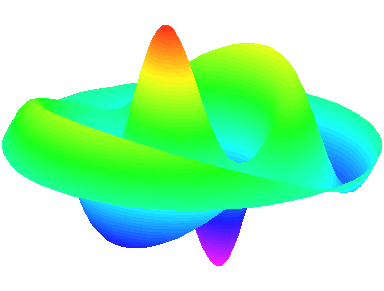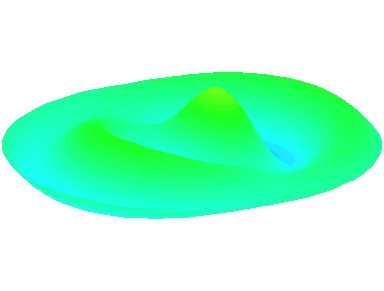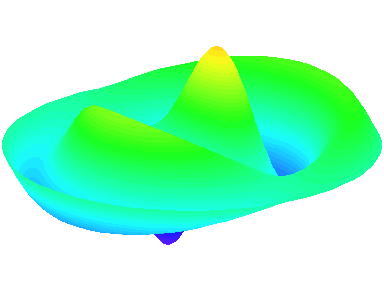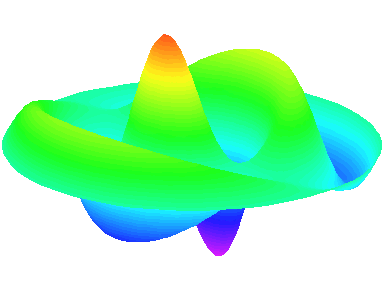
m=1.
n=3 : un troisième anneau nodal apparaît.
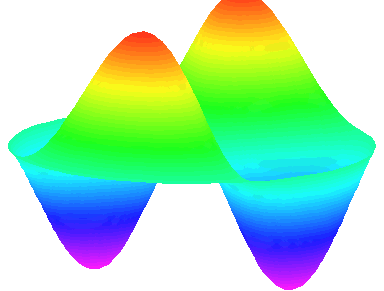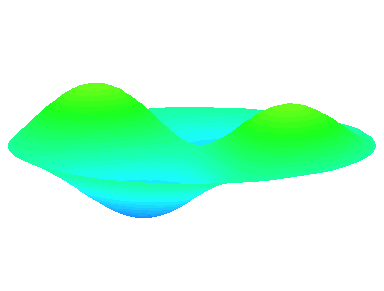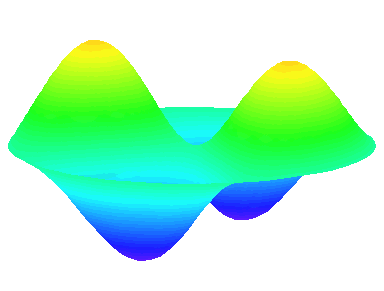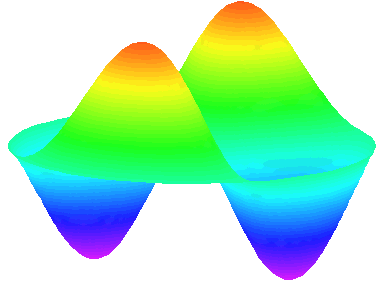
m=2 : il y a deux lignes nodales sur les diamètres \theta=0 et \theta=\frac{\pi}{2}.
n=1 : les autres nœuds se trouvent sur le cadre circulaire de la peau.
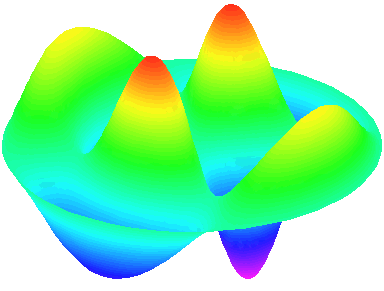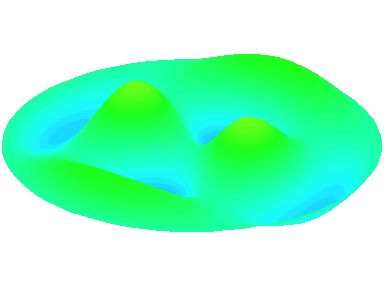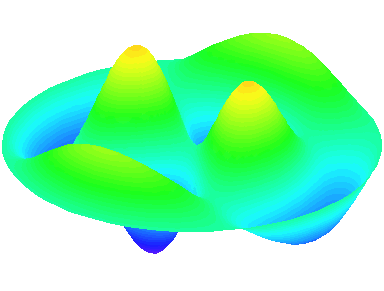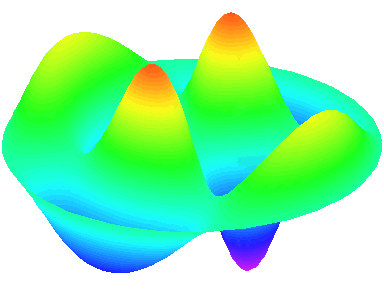
m=2.
n=2 : un autre anneau nodal apparaît.
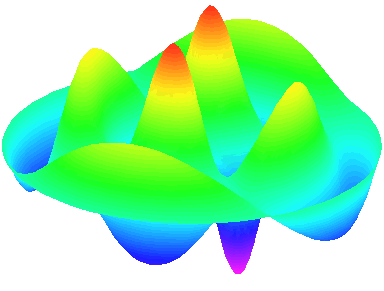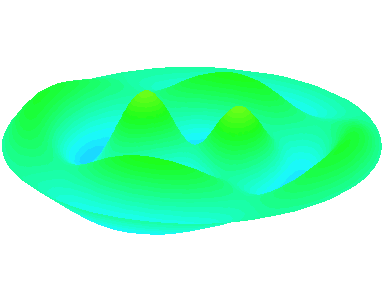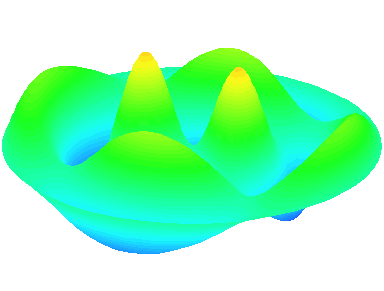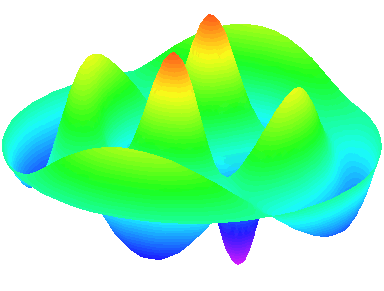
m=2.
n=2 : un troisième anneau nodal apparaît.
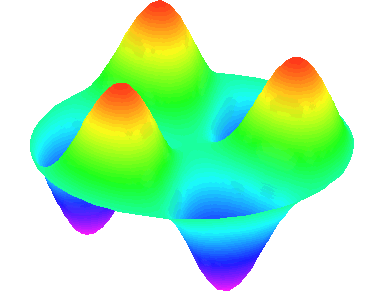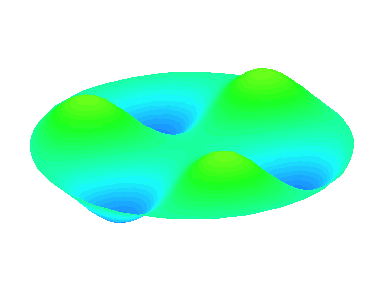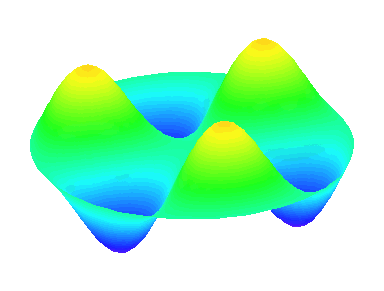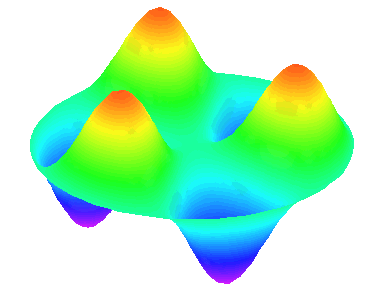
m=3 : il y a trois lignes nodales sur les diamètres \theta=0, \theta=\frac{\pi}{3} et \theta=\frac{2\pi}{3}.
n=1 : les autres nœuds se trouvent sur la cadre circulaire de la peau.
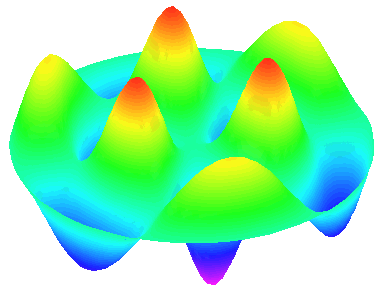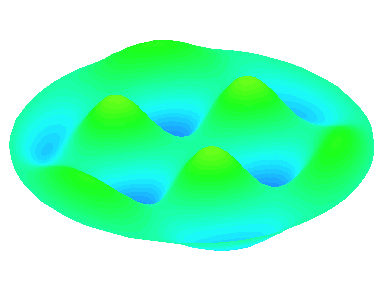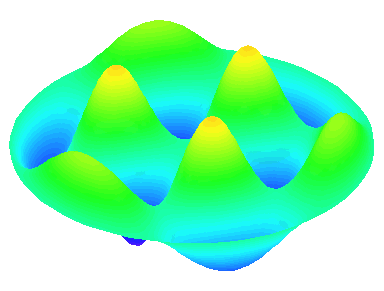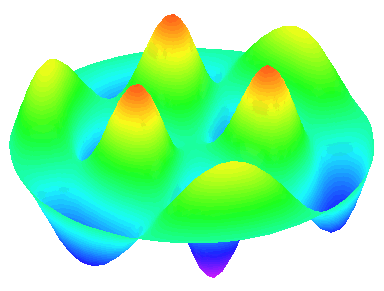
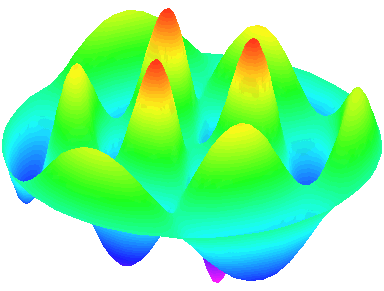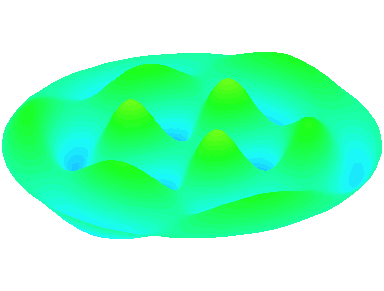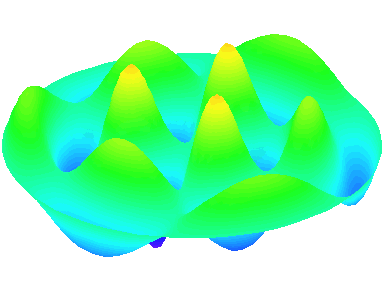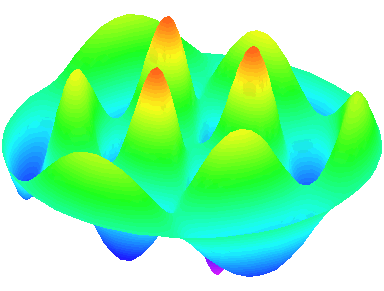
m=3.
n=2 : un autre anneau nodal apparaît.
m=3.
n=2 : un troisième anneau nodal apparaît.

Les mêmes modes que pour les animations. Les nœuds sont en noir, les ventres en blanc.
