CHIMIE
Applications du premier principe
Applications du premier principe
Applications du second principe
Applications du second principe
Déplacement d'équilibre
Déplacement d'équilibre
Étude cinétique des réactions redox
Étude cinétique des réactions redox
Fichiers Python à télécharger
Composés courants
Composés courants
Lecture d'un diagramme de Mollier
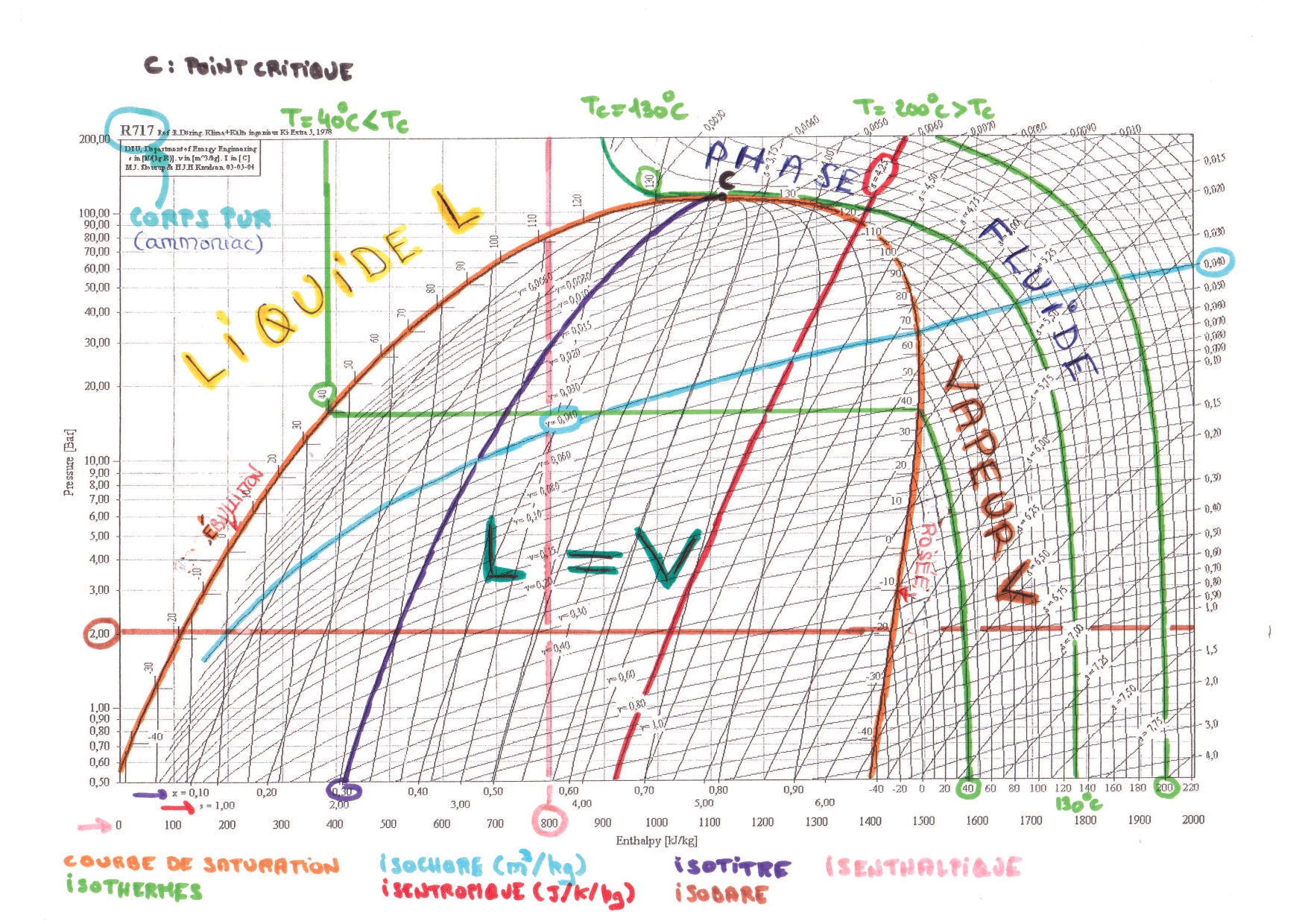
Point de fonctionnement d'un réacteur ouvert
Expériences Montaigne sur YouTube
Vibration de l’air dans un tube : expérience de Rüchardt
Le bouillant de Franklin
Compétences fondamentales
Applications du premier principe aux transformations physico-chimiques
- connaître la définition de l’avancement molaire d’une réaction, la notion de coefficients stœchiométriques algébriques.
- connaître la définition d’une grandeur de réaction, de l’état standard d’un système, d’une grandeur standard de réaction.
- connaître la définition de l’état standard de référence d’un élément chimique, de l’enthalpie standard de formation d’un composé ; savoir lire les tables thermodynamiques et appliquer la loi de Hess.
- savoir calculer l’enthalpie standard et l’énergie libre standard à toutes températures (grâce aux lois de Kirchhoff) ; connaître l’approximation d’Ellingham.
- savoir calculer une température de flamme ou d’explosion adiabatiques dans des situations diverses en décomposant la transformation en étapes simples.
Applications du second principe aux transformations physico-chimiques
- connaître les fonctions F et G et leurs propriétés, notamment que G décroit pour une transformation monobare et monotherme.
- pour un système en réaction chimique à pression et températures constantes, connaître la condition d’évolution et la condition d’équilibre .
- savoir trouver (loi de Hess) et à la température des tables, puis à toutes températures ; connaître et utiliser l’approximation d’Ellingham.
- connaître la définition du potentiel chimique, sa variation avec la pression, son expression dans les cas parfaits ainsi que les valeurs de l’activité d’un composé.
- savoir démontrer la loi de Guldberg et Waage. Savoir calculer une constante d’équilibre avec les tables. Savoir trouver la composition d’un système à l’équilibre en appliquant la loi de Guldberg et Waage.
- savoir énoncer exactement la définition de la variance d’un système chimique, savoir la calculer en dénombrant les paramètres d’état intensifs et les relations qui les lient.
- reconnaître les cas où il peut y avoir rupture d’équilibre, savoir tirer les conséquences de la valeur de la variance quant à la rupture d’un équilibre.
- savoir énoncer la loi de Van’t Hoff (influence de T sur un équilibre chimique), et de Le Châtelier (influence de p). Savoir si p est ou non facteur d’équilibre. Savoir mener l’étude théorique de l’optimisation d’un rendement.
Transitions de phase du corps pur
- connaître la condition d’équilibre d’un corps pur sous plusieurs phases (égalité des potentiels chimiques) ; savoir en tirer les conséquences sur la variance et sur le diagramme d’équilibre .
- connaître la définition et la signification des grandeurs molaires et massiques de transition de phase.
- prévoir l’évolution d’un corps pur diphasé hors d’équilibre.
- pour un équilibre liquide-vapeur, connaître l’allure des isothermes d’Andrews dans le diagramme ; savoir appliquer la règle des moments pour déterminer un titre massique en vapeur.
- savoir lire un diagramme de Mollier .
Étude thermodynamique des réactions d’oxydo-réduction : diagrammes potentiel – pH
- savoir déterminer les nombres d’oxydations extrêmes d’un élément à partir de sa position dans la classification périodique ; savoir calculer un nombre d’oxydation d’un élément dans une molécule ou un ion moléculaire, savoir équilibrer une demi-réaction redox.
- connaître les électrodes de première, seconde et troisième espèce, l’électrode standard à hydrogène et l’électrode au calomel saturée.
- connaître la loi de Nernst ; connaître l’inégalité reliant la variation d’enthalpie libre et le travail électrique. Connaître la relation entre la tension à vide d’une pile et l’enthalpie libre de réaction.
- savoir calculer la constante d’une réaction redox à l’aide des potentiels standard.
- connaître construction d’un diagramme potentiel-pH ; savoir distinguer domaine d’existence et de prédominance.
Étude cinétique des réactions d’oxydo-réduction : courbes intensité – potentiel
- savoir décrire le montage à trois électrodes permettant de mesurer une surtension.
- savoir associer vitesse de réaction électrochimique et intensité du courant ; reconnaître le caractère lent ou rapide d’un système à partir des courbes intensité-potentiel.
- savoir identifier les espèces électro-actives pouvant donner lieu à une limitation en courant par diffusion ; savoir identifier des paliers de diffusion sur des relevés expérimentaux.
- savoir donner l’allure qualitative de branches d’oxydation ou de réduction à partir de données de potentiels standard, de concentrations et de surtensions « de seuil ».
- piles. Savoir décrire le fonctionnement d’une pile à partir d’une mesure de tension à vide ou à partir des potentiels d’électrodes ; savoir déterminer la capacité d’une pile ; savoir utiliser les courbes intensité-potentiel pour expliquer le fonctionnement d’une pile électrochimique et prévoir la valeur de la tension à vide ; être capable de citer les paramètres influençant la résistance interne du dispositif électrochimique.
- électrolyseur. Savoir utiliser les courbes intensité-potentiel pour expliquer le fonctionnement d’un électrolyseur et prévoir la valeur de la tension de seuil ; savoir déterminer un rendement faradique à partir d’informations fournies concernant le dispositif étudié.
- savoir positionner qualitativement un potentiel mixte sur un tracé de courbes courant-potentiel ; savoir discuter la rapidité d’une réaction de cémentation ou d’attaque acide d’un métal.
- connaître les domaines d’immunité, de corrosion et de passivation d’un métal ; la corrosion différentielle, l’oxygénation différentielle (micro-piles), les techniques de protection du fer contre la corrosion (dont l’utilisation d’anodes sacrificielles).
F.A.Q
L’état réel d’un corps dépend de la température T, de la pression et de la composition du système qui le contient. Ainsi, une mol d’eau n’occupe pas le même volume si elle est pure que si on la mélange à une mol d’éthanol.
L’état standard d’un corps (gaz dans un mélange gazeux, liquide dans un mélange de liquide, solide dans un mélange de solides) correspond au corps pur à la même température T que dans l’état réel, et à une pression p^0=1\;\text{bar}.
La définition est différente pour un soluté, qui, dans l’état standard, est infiniment dilué dans le solvant (il n’est en interaction qu’avec le solvant), mais à une concentration C_{0}=1\;\text{mol}\cdot \text{L}^{-1}.
Un système est dans son état standard (souvent hypothétique) quand tous ses constituants sont dans leur état standard.
C’est l’enthalpie (libre) standard de la réaction de formation d’UNE mol de composé à partir des corps simples correspondant aux atomes qui le constituent, les plus stables à la température T considérée (corps dans leur état standard de référence).
Par exemple, \text{H}_2\text{O(g)} est constitué de \text{H} qui est le plus stable à 298 K sous la forme \text{H}_2\text{(g)}, et de \text{O} qui est le plus stable à 298 K sous la forme \text{O}_2\text{(g)}.
La réaction de formation de \text{H}_2\text{O(g)} est donc, à 298 K :
\text{H}_2\text{(g)}+\frac{1}{2}\text{O}_2\text{(g)}\longrightarrow \text{H}_2\text{O(g)}.
Ainsi, pour un corps simple dans son état standard de référence, \Delta_{\text{f}}H^0(T)=0 et \Delta_{\text{f}}G^0(T)=0 \;\forall T.
Elle consiste à négliger l’influence de la température sur \Delta_{\text{r}}H^0 et \Delta_{\text{r}}S^0, mais pas sur \Delta_{\text{r}}G^0 qui est alors une fonction affine de la température:
\Delta_{\text{r}}G^0(T)=\Delta_{\text{r}}H^0(T_0)-T\Delta_{\text{r}}S^0(T_0)
Elle est valable sur un domaine de température d’autant plus grand que la valeur absolue de \Delta_{\text{r}}C_p^0=\sum_{i}\nu_i C_{p\text{m}i}^0 est petite. Elle n’est pas valable sur un intervalle où l’un des corps de la réaction change de phase.
Pour déterminer une température de flamme (d’explosion), dans le cas d’une réaction totale et adiabatique, on décompose la transformation en deux parties :
- Réaction chimique à la température initiale (souvent T_0=298\;\text{K}, pour laquelle on connaît le \Delta_{\text{r}}H^0, ou le \Delta_{\text{r}}U^0 ). L’avancement est connu puisque la réaction est totale. Le réactif introduit en défaut disparaît entièrement.
- Passage des produits, réactifs restants, et corps inertes introduits, de la température initiale à la température finale. Il peut y avoir des transitions de phase. Il faut alors faire une hypothèse sur la température finale que l’on doit comparer aux températures de transition de phase.
Lorsque la réaction n’est pas totale, son avancement dépend de la température finale (d’après la loi de Guldberg et Waage), qui elle-même dépend de l’avancement puisqu’une certaine énergie est dégagée par mol de réaction. On doit alors dans une première partie amener les réactifs à la température finale, puis dans une deuxième partie réaliser la réaction à cette température.
Soit la réaction \sum_i \nu_i \text{A}_i =0.
L’enthalpie libre standard de réaction \Delta_{\text{r}}G^0(T) permet de calculer la constante d’une réaction K(T)=e^{-\frac{ \Delta_{\text{r}}G^0(T)}{RT}} . Elle est donc utile pour déterminer la composition du système à l’équilibre grâce à la loi de Guldberg et Waage K(T)=\prod_i a_{i\text{ éq}}^{\nu_i} .
L’enthalpie libre de réaction \Delta_{\text{r}}G=\Delta_{\text{r}}G^0(T)+RT\text{ln}Q=RT\text{ln}\frac{Q}{K} permet d’étudier le sens d’évolution de la réaction chimique. Si elle est positive : (Q>K), la réaction évolue dans le sens indirect, si elle est négative (Q<K), elle évolue dans le sens direct.
Q=\prod_i a_i^{\nu_i} est le quotient de réaction. Il n’est égal à K(T) qu’à l’équilibre thermodynamique, et que si il n’y a pas rupture d’équilibre (tous les corps de la réaction chimique existent à l’équilibre).
Il y a rupture d’équilibre quand un des corps de la réaction chimique disparaît. Il n’est donc pas présent dans le milieu réactionnel à l’équilibre thermodynamique.
Ce ne peut être le cas que pour un corps pur dans sa phase, donc dans un système hétérogène (qui contient plusieurs phases).
Il n’y a jamais rupture d’équilibre pour un système gazeux, ni pour une solution.
Une loi de modération stipule que le système réagit à une augmentation d’un des paramètres de façon à ce que ce paramètre diminue.
Pour la pression, c’est la loi de Le Chatelier : une augmentation de la pression déplace l’équilibre dans le sens de la diminution du nombre de mol de gaz, donc dans le sens où l’ordre augmente (\Delta_{\text{r}}S^0<0).
Pour la température, c’est la loi de Van’t Hoff qui traduit cette loi :
\frac{\text{dln}K}{\text{d}T}=\frac{\Delta_{\text{r}}H^0}{RT^2}. On en conclut qu’une augmentation de la température déplace l’équilibre dans le sens endothermique (si \Delta_{\text{r}}H^0>0, K est une fonction croissante de K, donc, à pression constante, la réaction se fait dans le sens direct).
La variance est le nombre de paramètres d’état INTENSIFS INDÉPENDANTS à l’ÉQUILIBRE thermodynamique.
Si elle vaut 0, il n’existe qu’une seule température telle que tous les corps coexistent. Si on ne se trouve pas à cette température, au moins un des corps disparaît (lequel ? Cela dépend des quantités de matière introduites). Dans le cas de deux réaction chimiques dans le système, elle ne peuvent être que successives si par exemple on introduit peu à peu un réactif, un corps inerte, que l’on fait varier p, T ou V…
Lorsqu’elle vaut 1, on peut choisir T mais p ne peut pas être quelconque : c’est une fonction de T.
Lorsqu’elle vaut 2, on peut fixer p et T.
Lorsqu’elle est supérieure à 2, on peut fixer p et T, et même se débrouiller en jouant sur les quantités de matière introduites pour fixer une ou plusieurs fractions molaires à l’équilibre.
Il faut faire attention pour la pression car elle peut ne pas être facteur d’équilibre si, pour toutes les réactions chimiques du système, les nombres de mol gazeux ne sont pas modifiés.
On donne souvent la constitution initiale de la pile, c’est-à-dire les quantités de matière introduites par le préparateur. Par exemple :
\text{(1) Ag(s) | AgNO}_3\text{(s)}\; 5\cdot 10^{-4} \text{ mol}\cdot\text{L}^{-1},\text{NH}_3 \; 0,2 \text{ mol}\cdot\text{L}^{-1}\textbf{ || }\text{ AgNO}_3\text{(s)}\; 5\cdot 10^{-4} \text{ mol}\cdot\text{L}^{-1},\text{NH}_3 \; 2 \text{ mol}\cdot\text{L}^{-1}\text{ | Ag(s) (2)}
Remarquons tout d’abord que le nitrate d’argent \text{ AgNO}_3\text{(s)} est un solide ionique. Quand on ne donne pas son K_{\text{s}}, c’est qu’il est entièrement dissout :
\text{ AgNO}_3\text{(s)}\rightarrow \text{Ag}^+ +\text{NO}_3^-. Il ne faut donc pas par la suite faire intervenir \text{ AgNO}_3 dans les réactions, car cette molécule n’existe pas ! On doit donc lire pour la demi-pile (1) :
\text{(1) Ag(s) | }\text{Ag}^+ \; 5\cdot 10^{-4} \text{ mol}\cdot\text{L}^{-1},\text{NO}_3^- \; 5\cdot 10^{-4} \text{ mol}\cdot\text{L}^{-1},\text{NH}_3 \; 0,2 \text{ mol}\cdot\text{L}^{-1}, et pour la demi-pile (2):
\text{Ag}^+ \; 5\cdot 10^{-4} \text{ mol}\cdot\text{L}^{-1},\text{NO}_3^- \; 5\cdot 10^{-4} \text{ mol}\cdot\text{L}^{-1},\text{NH}_3 \; 2 \text{ mol}\cdot\text{L}^{-1}\text{ | Ag(s) (2)}
Dans chaque demi-pile, il peut y avoir une réaction après introduction des réactifs, et ce avant même que la pile ne débite. Ici d’ailleurs, la pile ne débite pas : son but est de déterminer le nombre de coordination n du complexe \text{Ag(NH}_3)_n^{+} en mesurant la f.e.m à vide e=E_1-E_2.
Dans chaque demi-pile, il y a une réaction de complexation qui se produit entre les cations métalliques \text{Ag}^+ et les ligands \text{NH}_3 :
\text{Ag}^+ +n\text{NH}_3=\text{Ag(NH}_3)_n^{+}\text{ }\star , de constante \beta_n>>1.
Ainsi, ce que l’on a réellement dans les deux demi-piles lorsqu’on mesure e au voltmètre, ce sont des complexes, beaucoup plus stables que les cations \text{Ag}^+, qui sont donc présents à l’état de trace.
Néanmoins, la concentration initiale \left[\text{NH}_3\right]_0^{(2)} en ligand du côté (2), supérieure à celle \left[\text{NH}_3\right]_0^{(1)} du côté (1) implique que l’équilibre \star est plus déplacé vers la droite du côté (2) que du côté (1). Il en résulte qu’à l’équilibre, \left[\text{Ag}^+\right]_{\text{éq}}^{(1)}>\left[\text{Ag}^+\right]_{\text{éq}}^{(2)}, et donc que e=E_1-E_2>0.
Le couple ox/red qui intervient des deux côtés est le couple \text{Ag}^+/\text{Ag(s)}. La \frac{1}{2} équation redox correspondant à ce couple est :
\text{Ag}^+ +\text{e}^-=\text{Ag(s)}.
On ne peut appliquer la loi de Nernst qu’à l’équilibre dans chaque demi-pile, c’est-à-dire lorsque la pile ne débite pas. C’est le cas ici, et le potentiel de l’électrode (i), avec i \in \llbracket 1,2 \rrbracket, vaut :
E_i=E^0_{\text{Ag}^+/\text{Ag}}+0,06\cdot\text{log}\left[\text{Ag}^+\right]_{\text{éq}}^{(i)}
On a donc à vide e=E_1-E_2=0,06\cdot\text{log}\frac{\left[\text{Ag}^+\right]_{\text{éq}}^{(1)}}{\left[\text{Ag}^+\right]_{\text{éq}}^{(2)}}
\text{Ag}^+ étant le réactif limitant de chaque côté, la concentration à l’équilibre en complexe \text{Ag(NH}_3)_n^{+} est également la même :
\left[\text{Ag(NH}_3)_n^{+}\right]_\text{éq}=5\cdot 10^{-4} \text{ mol}\cdot\text{L}^{-1}. D’autre part, \text{NH}_3 étant introduit en large excès, sa concentration à l’équilibre est très proche de celle introduite. On obtient donc en appliquant la loi de Guldberg et Waage de chaque côté :
\beta_n=\frac{5\cdot 10^{-4}}{\left[\text{Ag}^+\right]_{\text{éq}}^{(1)}\times 0,2^n} et \beta_n=\frac{5\cdot 10^{-4}}{\left[\text{Ag}^+\right]_{\text{éq}}^{(2)}\times 2^n}. On en déduit \frac{\left[\text{Ag}^+\right]_{\text{éq}}^{(1)}}{\left[\text{Ag}^+\right]_{\text{éq}}^{(2)}}=10^n puis e=0,06\times n
Sachant que l’on mesure e=0,12\text{ V}, on en déduit n=2.
Le but de cette pile n’est pas de fournir de l’énergie, mais si elle débitait à travers une résistance R, le courant i dans cette résistance, orienté de (1) vers (2) serait positif. En effet, comme E_1>E_2, l’oxydant du côté (1) : \text{Ag}^+_{(1)}, est plus fort que l’oxydant du côté (2) : \text{Ag}^+_{(2)}, alors que le réducteur du côté (2) : \text{Ag(s)}_{(2)} , est plus fort que le réducteur du côté (1) : \text{Ag(s)}_{(1)}. Il s’agit d’une pile de concentration : le couple redox est le même des deux côtés, donc le potentiel standard aussi, mais il y a quand même une différence de potentiel car on n’est pas dans l’état standard.
La réaction du côté (1) est donc :
\text{Ag}^+_{(1)} +\text{e}^-\rightarrow \text{Ag(s)}_{(1)} . C’est une réduCtion : (1) est une Cathode. Le courant algébrique qui arrive dans cette demi-pile est i_\text{c}=-i<0.
La réaction du côté (2) est :
\text{Ag(s)}_{(2)}\rightarrow \text{Ag}^+_{(2)} +\text{e}^-. C’est une oxydAtion : (2) est une Anode. Le courant algébrique qui arrive dans cette demi-pile est i_\text{a}=i>0.
La réaction de fonctionnement de la pile est :
\text{Ag}^+_{(1)} +\text{Ag(s)}_{(2)}\rightarrow \text{Ag(s)}_{(1)}+\text{Ag}^+_{(2)} . Cette réaction tend à faire décroître \left[\text{Ag}^+\right]^{(1)}, donc à diminuer E_1, et à faire croître \left[\text{Ag}^+\right]^{(2)}, donc à augmenter E_2. Néanmoins, rappelons que la loi de Nernst n’est pas valable quand la pile débite (i\ne 0). Alors qu’elle a commencé à se décharger, il faut ouvrir le circuit pour que l’on puisse écrire e=E_1-E_2=0,06\cdot\text{log}\frac{\left[\text{Ag}^+\right]_{\text{éq}}^{(1)}}{\left[\text{Ag}^+\right]_{\text{éq}}^{(2)}}.
Lorsque i\ne 0, on a vu que la tension aux bornes de la pile vaut u=e-\eta-ri, où \eta est la surtension due aux phénomènes cinétiques, fonction croissante de i, et r la résistance de la pile.
Lorsque la pile arrête de débiter (i=0), la réaction de fonctionnement de la pile est équilibrée :
\text{Ag}^+_{(1)} +\text{Ag(s)}_{(2)}= \text{Ag(s)}_{(1)}+\text{Ag}^+_{(2)} , et on a E_1=E_2, soit \left[\text{Ag}^+\right]_{\text{éq}}^{(1)}=\left[\text{Ag}^+\right]_{\text{éq}}^{(2)}.
Prenons l’exemple de l’oxydation d’un métal, le magnésium, par l’eau.
Le potentiel standard du couple \text{Mg}^{2+}/\text{Mg(s)} est E^0_2=-2,37\text{ V}, celui du couple \text{H}^+/\text{H}_2\text{(g)} est E^0_1=0,00\text{ V}.
Pour la \frac{1}{2} équation redox de l’oxydation du magnésium, le problème d’équilibrer avec \text{H}^+ ou des \text{OH}^- ne se pose pas :
\text{Mg(s)}\rightarrow \text{Mg}^{2+}+2\text{e}^-.
Pour la \frac{1}{2} équation redox de réduction de l’eau, le plus simple est d’équilibrer avec \text{H}^+ :
2\text{H}^++2\text{e}^-\rightarrow \text{H}_2\text{(g)}
On obtient l’équation redox :
\text{Mg(s)}+2\text{H}^+\rightarrow \text{Mg}^{2+}+\text{H}_2\text{(g)}, dont la constante est K=10^{\frac{E^0_1-E^0_2}{0,03}}=3,16\cdot 10^{39}>>1
Si on connaît les quantités de matière initiales et que l’on veut les déterminer à l’équilibre, il suffit de faire un bilan de matière sous la réaction chimique et d’appliquer la loi de Guldberg et Waage. Si on a introduit du magnésium solide en milieu acide, la réaction précédente a bien lieu.
Par exemple si on a introduit 4\cdot 10^{-5}\text{ mol} de \text{Mg(s)} dans un litre d’eau de \text{p}H=0, le magnésium disparaît totalement. La concentration en \text{H}^+ est très peu modifiée, et on forme 4\cdot 10^{-5}\text{ mol} de \text{Mg}^{2+} et de \text{H}_2\text{(g)}.
En revanche, si la même quantité de magnésium est placée dans un litre d’eau de \text{p}H=7, la réaction redox écrite précédemment n’est plus la réaction prépondérante : elle ne fait pas intervenir des réactifs majoritairement introduits car \left[\text{H}^+\right]=10^{-7}\text{ mol}\cdot \text{L}^{-1}. La réaction d’autoprotolyse de l’eau n’est pas négligeable.
On obtient alors la réaction prépondérante en écrivant la \frac{1}{2} équation redox de réduction de l’eau avec non plus \text{H}^+ mais \text{H}_2\text{O}. Il suffit « d’ajouter » deux \text{OH}^- de chaque côté :
2\text{H}_2\text{O}+2\text{e}^-\rightarrow \text{H}_2\text{(g)}+2\text{OH}^-
On obtient l’équation redox :
\text{Mg(s)}+2\text{H}_2\text{O}\rightarrow \text{Mg}^{2+}+\text{H}_2\text{(g)}+2\text{OH}^-, dont la constante est K’=K\times K_\text{e}^2=3,16\cdot 10^{11}. La réaction reste totale, mais lente comme on l’a vu en T.P (c’est dû à la forte surtension anodique à vide de \text{H}_2\text{(g)} sur électrode de \text{Mg(s)}).
\text{Mg(s)} finit donc par disparaître totalement, et on forme 4\cdot 10^{-5}\text{ mol} de \text{Mg}^{2+} et de \text{H}_2\text{(g)}, et 8\cdot 10^{-}\text{ mol} de \text{OH}^- par litre de solution, soit \text{p}H=9,9. Le passage de milieu neutre à milieu basique se caractérise aisément en ajoutant quelques gouttes d’indicateur coloré.
En résumé, il vaut mieux toujours chercher à écrire la réaction prépondérante entre réactifs majoritairement introduits et qui amène aux produits les plus stables. Quelquefois, plusieurs réactions sont à prendre en compte mais c’est rare dans les sujets de concours.
