PHYSIQUE DES ONDES
Compléments de cours
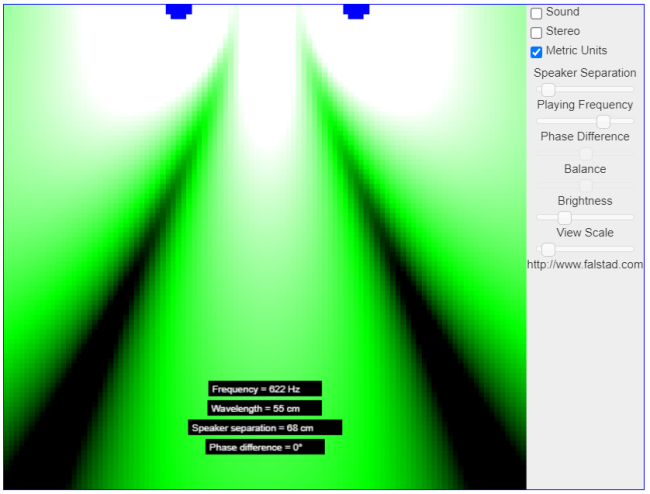
Falstad.com Site en anglais très complet pour visualiser des phénomènes ondulatoires 2D, faire des interférences sonores avec les enceintes de votre ordinateur…
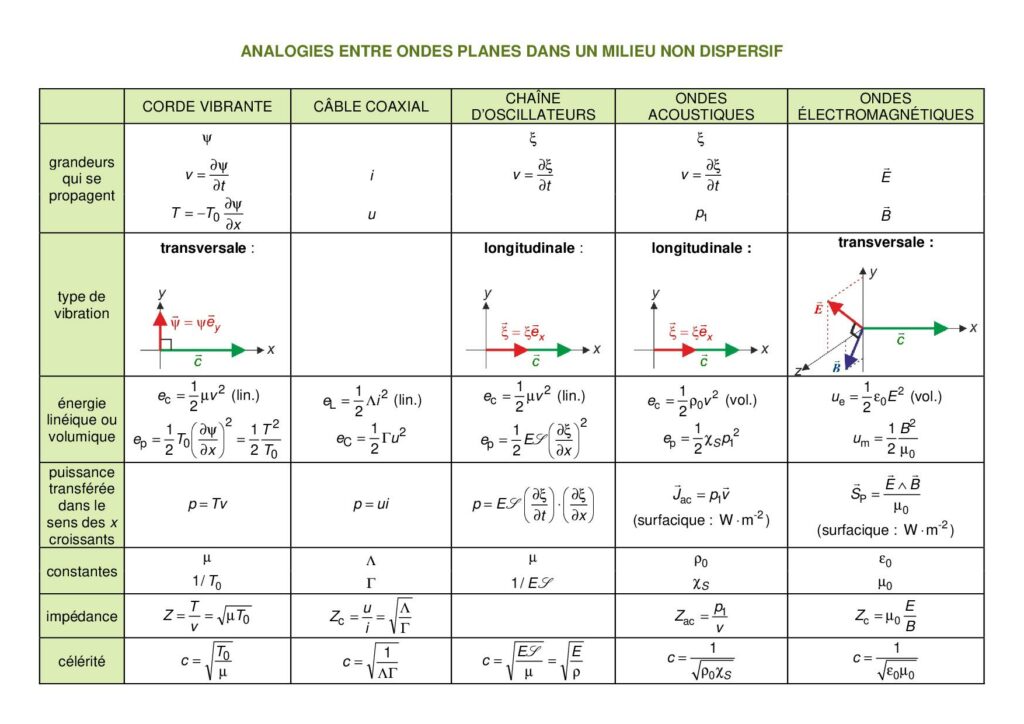
Analogies entre ondes planes
Musique et gamme tempérée
Lorsqu’on joue une note d’une certaine hauteur, on obtient la même note en jouant la fréquence double. Ces deux notes sont séparées d’une octave (une octave correspond à une multiplication par 2, là où une décade correspond à une multiplication par 10). Par exemple, le \text{la}_1 de la première octave correspond à une fréquence de 110,0 Hz, le \text{la}_2 de la deuxième octave à 220,0 Hz, le \text{la}_3 à 440,0 Hz…
Dans la gamme tempérée, chaque octave est elle-même séparée en douze demi-tons régulièrement espacés, c’est-à-dire qu’on passe d’une note à la suivante en multipliant sa fréquence par 2^{1/12}. On donne un nom à seulement certaines de ces notes (do, ré, mi, fa, sol, la, si). Le symbole dièse (\sharp) appliqué à une note permet de passer au demi-ton suivant ; le symbole bémol (\flat) appliqué à une note permet de passer au demi-ton précédent.
Par exemple, pour la première octave :
On peut remarquer que 2^{1/12} étant irrationnel, les rapports de fréquences pour les notes de la gamme tempérée ne sont pas des rapports d’entiers (sauf quand ce rapport vaut 2). Dans le spectre d’une note, les fréquences des harmoniques sont des multiples de la fréquence fondamentale, et peuvent différer sensiblement de la fréquence des notes de la gamme. Prenons l’exemple d’un \text{do}_1 de fréquence fondamentale f_0. Le rapport de fréquence f/f_0 vaut un entier n pour l’harmonique de rang n. Si ce rapport était une note de la gamme tempérée, il existerait un entier p tel que n=2^{p/12} \iff p=12\text{log}_2(n). Calculons pour n \in \llbracket 1,8 \rrbracket la valeur de 12\text{log}_2(n) et comparons-la à la note correspondant à l’entier p le plus proche :
L’harmonique de rang 5 est légèrement dissonant, et s’écarte de la note la plus proche, le \text{mi}_3, et l’harmonique de rang 7 s’écarte encore plus de la note la plus proche, le \text{la}_3\sharp, ce qui peut être désagréable pour une oreille entrainée (la différence n’est pas évidente comme on peut le constater avec les sons proposés ci-dessous).
Si un de ces harmoniques, qui apparaît « naturellement » quand on joue un \text{do}_1 avec un instrument harmonique (qui produit des fréquences multiples d’une fréquence fondamentale, comme la guitare ou le piano), est entendu en même temps que la note la plus proche, il en résulte des battements désagréables. C’est le cas par exemple si l’harmonique de rang 5 d’un \text{do}_1, de fréquence 5\times 65,4=327,0 \text{Hz} est entendu en même temps que la note la plus proche : un \text{mi}_3 de fréquence 2^{28/12}\times 65,4=329,6 \text{Hz}. Voici ce qu’on entendrait (l’effet est ici exagéré du fait que les deux sons sinusoïdaux ont été pris de même amplitude alors que les amplitudes des harmoniques sont souvent d’autant plus faibles que le rang de l’harmonique est élevé) :
Sinusoïde à 327,0 Hz
Sinusoïde à 329,6 Hz
Battements résultants
Recommençons avec l’harmonique de rang 7 d’un \text{do}_1, de fréquence 7\times 65,4=457,8 \text{Hz}, et la note la plus proche : un \text{la}_3\sharp de fréquence 2^{34/12}\times 65,4=466,1 \text{Hz}. Voici ce qu’on entendrait :
Sinusoïde à 457,8 Hz
Sinusoïde à 466,1 Hz
Battements résultants
Capacité numérique 7
Compétences fondamentales
Phénomènes ondulatoires non dispersifs
- savoir établir l’équation de d’Alembert pour une corde vibrante dans l’approximation linéaire où la perturbation \left(\psi(x,t),\theta(x,t)\right), où \theta(x,t) est l’angle que fait à t la tangente en x à la corde avec la corde au repos, sont considérés comme des infiniment petits du premier ordre.
- connaître l’équation de d’Alembert et ses propriétés (réversibilité, linéarité), les solutions en F\left(t-\frac{x}{c}\right)+G\left(t+\frac{x}{c}\right) pour une onde plane, la signification du terme F\left(t-\frac{x}{c}\right) : onde plane progressive se propageant sans déformation à la célérité c dans le sens des x croissants, sa décomposition en O.P.P.H (harmoniques) : s_0\text{cos}(\omega t-kx) avec \overrightarrow{k}=\frac{\omega}{c}\overrightarrow{e}_x=\frac{2\pi}{\lambda}\overrightarrow{e}_x vecteur d’onde : double périodicité temporelle (T) et spatiale(\lambda) avec \lambda=cT ; connaître la notation complexe (utilisable seulement avec des opérateurs linéaires).
- connaître les solutions d’ondes planes stationnaires harmoniques s_0\text{sin}(kx+\alpha)\text{cos}(\omega t+\varphi) avec k=\frac{\omega}{c}, la notion de nœuds et ventres de vibration, de modes propres de vibration (toutes les grandeurs ondulatoires sont sinusoïdales de même pulsation \omega) et leur utilité pour la recherche d’une onde solution de l’équation de d’Alembert avec des conditions aux limites et initiales imposées.
- connaître le dispositif de la corde de Melde, ses résonances.
- connaître la description du câble coaxial, savoir retrouver les équations de couplage entre tension et intensité, l’équation de d’Alembert, l’impédance caractéristique, les coefficients de réflexion en tension ou en intensité sur une impédance terminale.
Ondes acoustiques dans les fluides
- savoir établir (à 3D et à 1D) les équations de couplage pour la perturbation \left(p_1,\rho_1,\overrightarrow{v}\right), considérée comme un infiniment petit du premier ordre (approximation acoustique linéaire), puis l’équation de d’Alembert pour p_1 et \overrightarrow{v}. En déduire l’expression de la célérité c=\frac{1}{\sqrt{\rho_0\chi _S}} d’une onde sonore dans un fluide quelconque, puis celle c=\sqrt{\frac{\gamma RT_0}{M}} dans un gaz parfait ; connaître les ordres de grandeurs de c pour l’air et l’eau.
- connaître les expressions de la densité volumique d’énergie acoustique et du vecteur densité de courant énergétique, ainsi que de l’intensité sonore. Connaître le domaine spectral du son perçu par l’oreille et savoir calculer numériquement la perturbation acoustique pour une intensité sonore donnée.
- pour une onde plane progressive dans un tuyau sonore, savoir retrouver l’impédance acoustique et traiter les problèmes de réflexion et transmission lors d’une discontinuité de structure.
- connaître les solutions pour la surpression dans le cas d’une onde sphérique; savoir utiliser le P.F.D linéarisé appliqué à une particule fluide pour en déduire la vitesse.
- connaître l’effet Doppler et ses applications, savoir calculer le changement de fréquence.
Propagation des ondes électromagnétiques dans le vide
- savoir établir l’équation de d’Alembert pour \overrightarrow{E} et \overrightarrow{B} dans le vide.
savoir déterminer la structure d’une onde plane progressive, sa densité d’énergie, son intensité.
pour une O.P.P.H, connaître les différents états de polarisation, la notation complexe (seulement utilisable avec des opérateurs linéaires).
connaître la classification des ondes électromagnétiques selon leur domaine spectral, le domaine perçu par l’œil, avoir des notions sur l’émission de la lumière et la propagation dans un milieu transparent.
savoir déterminer l’onde réfléchie normalement sur un conducteur parfait, l’onde stationnaire résultante ; savoir effectuer un bilan d’énergie électromagnétique et photonique.
Dispersion, absorption, atténuation / ondes électromagnétiques dans les plasmas et les conducteurs
connaître la technique de recherche d’ondes planes se propageant dans un milieu linéaire quelconque : utilisation de la notation complexe \underline{s}=s_0 e^{i(\omega t-kx)}, et recherche de k sous la forme k=k^{\prime}(\omega)+ik^{\prime\prime}(\omega) ; connaître pour une telle onde vectorielle l’expression de la dérivée temporelle \frac{\partial\underline{\overrightarrow{A}}}{\partial t}=i\omega \underline{\overrightarrow{A}} , des opérateurs \text{div}\underline{\overrightarrow{A}}=-i \overrightarrow{k}\cdot \underline{\overrightarrow{A}} et \overrightarrow{\text{rot}}\underline{\overrightarrow{A}}=-i \overrightarrow{k}\wedge \underline{\overrightarrow{A}} .
toujours pour une telle onde plane, savoir déterminer la relation de dispersion entre k et \omega; connaître la définition de la vitesse de phase et de groupe et savoir les calculer grâce à la relation de dispersion ; savoir interpréter k^{\prime}=0 (l’onde est alors stationnaire), et k^{\prime\prime}\neq 0 (il y a alors atténuation ou absorption).
cas d’un plasma : connaître le modèle microscopique, savoir obtenir et interpréter la relation de dispersion.
cas d’un conducteur : connaître le modèle microscopique, savoir obtenir et interpréter la relation de dispersion, savoir retrouver l’épaisseur de peau ; connaître les propriétés d’un conducteur parfait.d
F.A.Q
Soient R et R’ deux référentiels galiléens. R’ est en translation rectiligne uniforme avec la vitesse \overrightarrow{u} par rapport à R.
Une particule de charge q (indépendante du référentiel) doit subir la même force de Lorentz dans les deux référentiels :
\overrightarrow{F’}=q\left(\overrightarrow{E’}+\overrightarrow{v’}\wedge \overrightarrow{B’}\right)=\overrightarrow{F}=q\left(\overrightarrow{E}+\overrightarrow{v}\wedge \overrightarrow{B}\right)=q\left(\overrightarrow{E}+(\overrightarrow{v’}+\overrightarrow{u})\wedge \overrightarrow{B}\right)
où les grandeurs dans R’ sont notées avec un « prime ».
Cette relation doit être vérifiée \forall \; \overrightarrow{v}, ce qui entraîne :
\begin{cases} \overrightarrow{B’} &=\overrightarrow{B}\\\overrightarrow{E’}&=\overrightarrow{E}+\overrightarrow{u}\wedge \overrightarrow{B} \end{cases}
Le changement de référentiel galiléen n’est cependant pas compatible avec les lois de l’électromagnétisme car il ne laisse pas invariantes les équations de Maxwell. Elles ne le sont que par un changement de référentiel relativiste. Les relations obtenues entre les champs dans R’ et R ne sont donc valables que si u<<c.
Le modèle du plasma dilué dans lequel se propage une onde électromagnétique plane, progressive et harmonique (considérée comme une petite perturbation) amène à la relation \overrightarrow{\underline{J}}=\frac{n_0 e^2}{i m\omega}\overrightarrow{\underline{E}} .
L’équation locale de conservation de la charge fournit :
\frac{\partial \underline{\rho}}{\partial t} +\text{div} \overrightarrow{\underline{J}}=0 , soit :
i\omega \underline{\rho} +\frac{n_0 e^2}{i m\omega}\text{div}\overrightarrow{\underline{E}} =0 .
L’équation de Mawell-Gauss \text{div}\overrightarrow{\underline{E}} =\frac{\underline{\rho}}{\epsilon_0} permet d’éliminer \overrightarrow{\underline{E}} :
i\omega \underline{\rho} +\frac{n_0 e^2}{i\epsilon_0 m\omega}\underline{\rho} =0 .
On constate qu’une charge volumique non nulle n’est possible que si :
\omega=\omega_{\text{p}}=\sqrt{\frac{n_0 e^2}{\epsilon_0 m}} , pulsation plasma.
L’équation de Maxwell-Ampère s’écrit :
\text{rot}\overrightarrow{\underline{B}}=\mu_0\left(\overrightarrow{\underline{J}}+\epsilon_0 \frac{\partial \overrightarrow{\underline{E}}}{\partial t}\right), soit :
-i\overrightarrow {k}\wedge\overrightarrow{\underline{B}}=\mu_0\left(\underset{=0}{\frac{n_0 e^2}{i m\omega}+i\omega\epsilon_0}\right) \overrightarrow{\underline{E}}.
Le champ magnétique est donc colinéaire à \overrightarrow {k}, mais l’équation de Maxwell-Thomson -i\overrightarrow {k}\cdot\overrightarrow{\underline{B}}=0 montre que \overrightarrow{B} \perp \overrightarrow {k} , donc \overrightarrow{B} = \overrightarrow {0}.
L’équation de Maxwell-Faraday montre que -i\overrightarrow {k}\wedge\overrightarrow{\underline{E}}=-i\omega\overrightarrow{\underline{B}}=\overrightarrow {0} , donc \overrightarrow{E} est colinéaire à \overrightarrow{k} .
Finalement : une onde longitudinale (le champ électrique est colinéaire à la direction de propagation) de champ magnétique nul et de pulsation plasma \omega=\omega_{\text{p}}=\sqrt{\frac{n_0 e^2}{\epsilon_0 m}} peut se propager dans un plasma dilué, qui est alors non neutre (la charge volumique oscille).